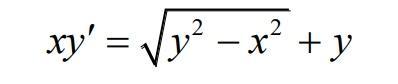Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
xy'(x)=√(y(x)^2 -x^2) +y(x)
x•dy(x)/dx=√(-x^2 +y(x)^2) +y(x)
Возьмем y(x)=xv(x), тогда:
dy(x)/dx=x•dv(x)/dx +v(x)
x(x•dv(x)/dx +v(x)=√(-x^2 +x^2 •v(x)^2) +xv(x)
x(x•dv(x)/dx +v(x)=x(√(v(x)^2 -1) +v(x))
Находим для:
dv(x)/dx=(√(v(x)^2 -1))/x
Делим обе стороны на числитель правой стороны:
(dv(x)/dx)/√(v(x)^2 -1)=1/x
Теперь интегрируем обе стороны по отношению к х:
∫(dv(x)/dx)/√(v(x)^2 -1) •dx=∫1/x •dx
log(√(v(x)^2 -1) +v(x))=log(x)+c, где с - произвольная константа
Находим для:
v(x)=(e^-с +e^c •x^2)/2x
Упрощаем произвольные константы:
v(x)=1/2cx +cx/2
Вернемся к y(x)=xv(x) для подстановки:
y(x)=x(1/2cx +cx/2)
Упрощаем произвольные константы и получаем ответ:
y(x)=1/4c +cx^2
Похожие вопросы
1 год назад
8 лет назад
8 лет назад
9 лет назад