Предмет: Алгебра
Автор: Purzil
Вопрос задан 7 лет назад

< >

Прошу помочь найти площадь фигуры,ограниченной линиями y=4x-x^2,y=0

Ответы

Ответ дал: takushnir

0

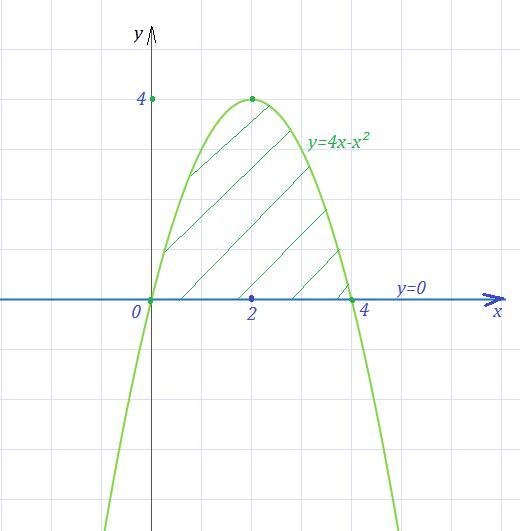
найдем пределы интегрирования, решив уравнение. 4х-х²=0, х=0; х=4

По формуле Ньютона- Лейбница найдем определенный интеграл от нуля до четырех от разности 4х-х²-0, получим 2х²-х³/3, подставим пределы интегрирования. 2*16-64/3-0+0=32-21целая 1/3=10 целых 2/3

Ответ дал: NNNLLL54

0

x^3/3 при x=4 вычислено неверно

Ответ дал: NNNLLL54

0

$y=4x-x^2; ; ,; ; y=0\\4x-x^2=0; ,; ; x(4-x)=0; ; to ; ; x_1=0; ,; x_2=4\\S=intlimits^4_0, (4x-x^2), dx=(4cdot frac{x^2}{2}-frac{x^3}{3})Big |_0^4=2cdot 16-frac{64}{3}=32-frac{64}{3}=frac{32}{3}=10frac{2}{3}$

Приложения:

Похожие вопросы

Английский язык

2 года назад

срочно плиззззззз!!!!!!!

Английский язык

2 года назад

Помогите с упражнением 221 и 223.

Математика

2 года назад

човен проплив 21 км, що становить 7/15 наміченого маршруту. Скільки кілометрів повинен пропливти човен?

Английский язык

2 года назад

Помогите решить английский!!! Choose the correct form: 1. Have you ever read/been reading this book? 2. She has learnt/been learning German for six months. 3. I’ve been/been being here for 3

Математика

8 лет назад

Помогите, очень нужно. Срочно!!!!!!!!

Алгебра

8 лет назад

Cделайте пожалуйста 10 вопрос! Даю 20 баллов

Математика

9 лет назад

Городской автобус проехал 155 км и ему осталось проехать еще 87 км.Какое расстояние должен преодолеть автобус? Развяжи задачу, сложивши уравнение.

Математика

9 лет назад

тык тортбурыштын екы карама карсы кабыргасы жалпы узындыгы 18см онын кабыргасы 8см тык тортбурышттын периметр жане ауданын тап