Предмет: Алгебра
Автор: crafalska
Вопрос задан 7 лет назад

Знайдіть площу трикутника ,утвореного дотичними до графіка функції y=x^3-3x^2-1, провединими в точках з абсцисами x1=1; x2=-1; x3=0. Будь ласка

Ответы

Ответ дал: WhatYouNeed

$f(x)=x^3-3x^2-1;x_1=1;x_2=-1;x_3=0\f'(x)=3x^2-6x$

$y_{kx_1}=f'(x_1)(x-x_1)+f(x_1)=\(3*1^2-6*1)(x-1)+(1^3-3*1^2-1)=\-3(x-1)-3=-3x\\y_{kx_2}=f'(x_2)(x-x_2)+f(x_2)=\(3*(-1)^2-6*(-1))(x+1)+((-1)^3-3*(-1)^2-1)=\9(x+1)-5=9x+4\\y_{kx_3}=f'(x_3)(x-x_3)+f(x_3)=\(3*0^2-6*0)(x-0)+(0^3-3*0-1)=\0*x-1=-1$

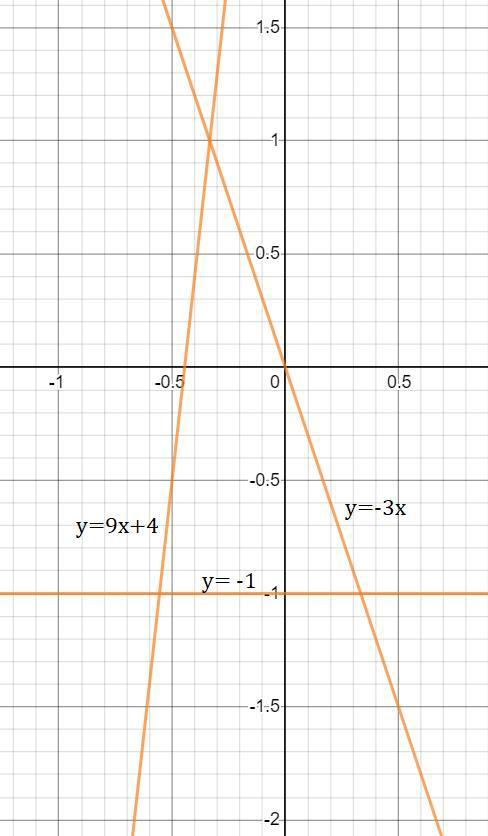
Построим прямые на координатной плоскости (по двум точкам).

Смотри вниз.

Найдём площадь через высоту треугольника и его основание. Основание параллельно оси Ох, поэтому высота будет параллельна оси Оу и всё просто. Если, что основанием я обозначил ту сторону треугольника, которая самая нижняя.

H-высота, l-основание, S-площадь.

$9x+4=-3x;x=frac{-4}{12}=frac{-1}{3};\\y=-3*frac{-1}{3}=1,(-frac{1}{3};1)\\H=|1-(-1)|=2\\9x+4=-1;x=frac{-5}{9}\\-3x=-1;x=frac{1}{3}\\l=|-frac{5}{9}-frac{1}{3}|=frac{5+3}{9}=frac{8}{9}\\S=frac{1}{2}*frac{8}{9}*2=frac{8}{9}$