Предмет: Геометрия
Автор: vladkraev4
Вопрос задан 7 лет назад

висота правильной чотирех-стороной пирамиды 12 см а сторона основи 10 см знайдить бичну поверхню этой пирамиды

Ответы

Ответ дал: WhatYouNeed

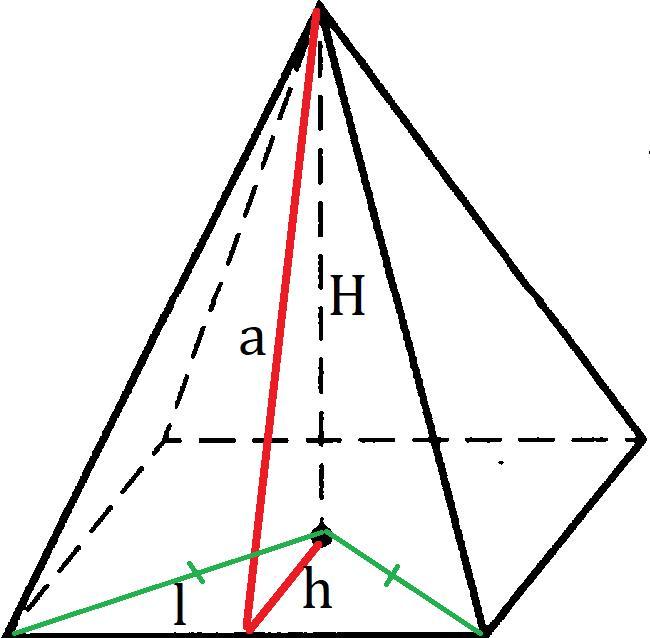
У правильной четырёхугольной пирамиды в основании лежит квадрат, а основание высота пирамиды является центром квадрата. Зная сторону квадрата (l) можно найти его диагональ - 10√2. Найдём высоту (в одном из 4 треугольников, которые образуются при пересечении диагоналей квадрата) из середины квадрата:

$h^2=(frac{10sqrt{2}}{2})^2-(frac{10}{2})^2=5^2\h=5$

В принципе это и так логично, ведь диагональ квадрата составляет 45° с его сторонами. Теперь мы можем найти апофему пирамиды (её основание будет совпадать с основание недавно проведённой высоты т.к. это высота и медиана в равнобедренном треугольнике)

a - апофема (высота боковой грани).

$a^2=H^2+h^2=12^2+5^2=13^2;a=13$