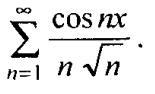Найти область сходимости функционального ряда.

Этот ряд при любом х меньше чем ряд 1/(n^1.5), который сходится, потому что 1.5>1

Так что область сходимости - все вещественные числа

Ответ:

х∈(-∞;  +∞)

Пошаговое объяснение:

Используем признак Вейерштрасса

Для  ряда

существует мажорантный ряд

Известно, что последний ряд сходится, так как степень в знаменателе больше единицы. Значит существует мажорантный сходящийся ряд по отношению к исходному знакопеременному ряду. По признаку Вейерштрасса исходный ряд сходится. Здесь |cos nx|≤1 независимо от х в поле действительных чисел. Значит х∈R.