вычислите площадь фигуры, ограниченной линиями, сделать рисунок y=x(x-6), y=0. ОЧЕНЬ ПРОШУ!! ​

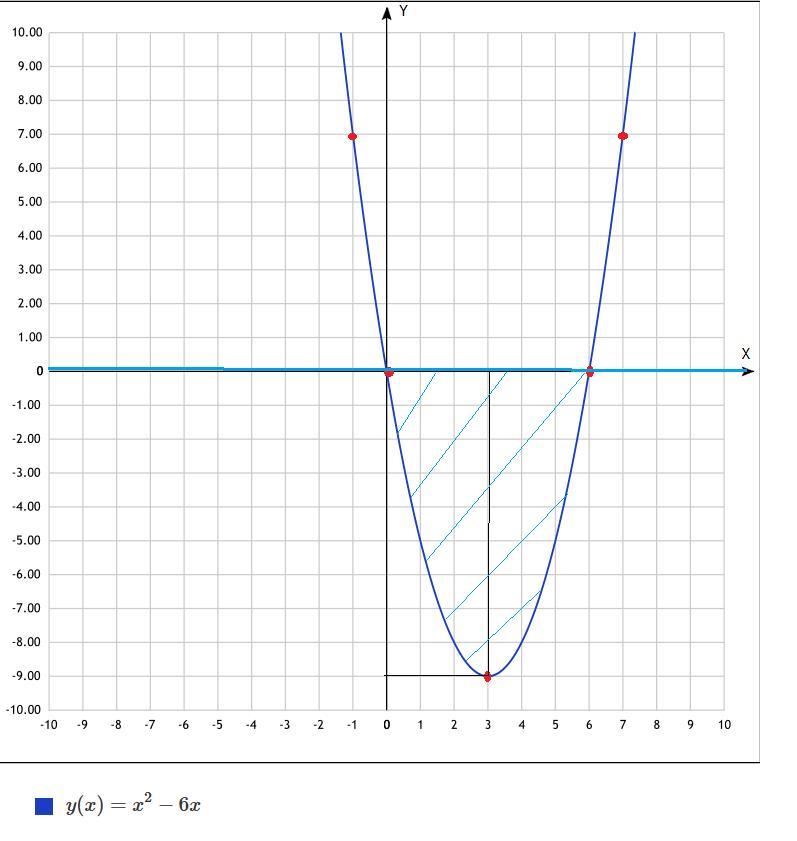
y=x(x-6)=x^2-6x-парабола , пересекает ось х (y=0) при x=0 и 6

0=x(x-6); x1=0; x2=6

вершина параболы x0=-b/(2a)

общий вид параболы y=ax^2+bx+c

в данном примере a=1; b=-6; c=0

x0=-(-6)/2=3

y0=y(3)=3^2-6*3=9-18=-9

(3;-9)-вершина параболы, построю ее

(0;0);(6;0)-нули функции

можно взять еще 2 точки y(-1)=1+6=7; y(7)=49-42=7

(-1;7);(7;7)

график y=0-это ось х

фигура, ограниченная этими кривыми, на рисунке указана штриховкой

Чтобы вычислить площадь ее, надо взять интеграл от разности функций, из верхней вычесть нижнюю

Выше лежит у=0, ниже у=x^2-6x

s=∫(0-(x^2-6x))dx= -∫(x^2-6x)dx= -(x^3/3-6*x^2/2)= -x^3/3+3x^2=

подставлю пределы интегрирования- х меняется от 0 до 6

= -6^3/3+3*6^2-(0+0)= -72+108=36

Ответ S=36