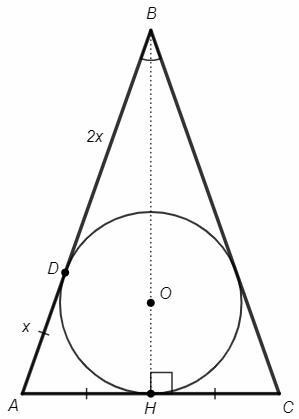
В равнобедренный треугольник ABC(AB=BC)вписана окружность.Точка касания Д делит сторону AB в отношении 1:2,считая от вершины A.Найдите сторону AB,если сторона AC равна 6 см.
Ответы
Ответ дал:
0
Высота BH к основанию равнобедренного треугольника является медианой и биссектрисой. Центр вписанной окружности О лежит на биссектрисе. OH - перпендикуляр из центра к основанию, H - точка касания.
AH=AC/2 =3
Отрезки касательных из одной точки равны, AD=AH =3
AD=x, BD=2x => AB=3x =9
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад