Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Приложения:
Ответ дал:
0
Здравствуйте, можете помочь с алгеброй?
Ответ дал:
0
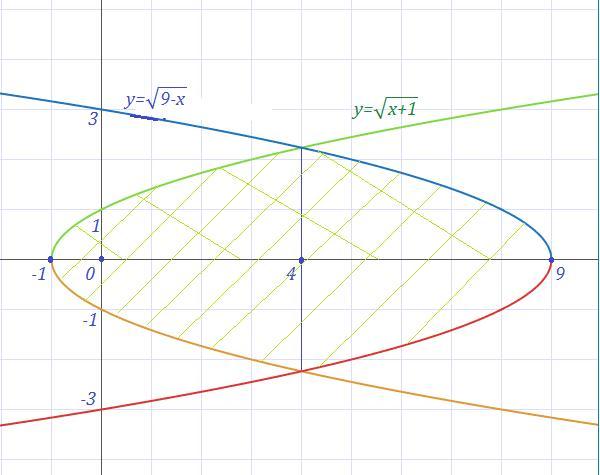
Ответ: S=29.81 кв. ед.
Пошаговое объяснение:
y²=x+1 ⇒ x=y²-1
y²=9-x ⇒ x=9-y²
y²-1=9-y²
2y²=10 |÷2
y²=5
y₁=-√5 y₂=√5
S=₋√₅∫√⁵(9-y²-(y²-1))dx=₋√₅∫√⁵(10-2y²)dx=10y-2*y³/3 √₋₅|√⁵=
=10*√5-2*(√5)³/3-(10*(-√5)-2*(-√5)³/3)=2*(10*√5-2*(√5)³/3)=
=2*√5*(10-2*5/3)=2*√5*(3*10-10)/3=
2*√5*(30-10)/3=2*√5*20/3=40*√5/3≈29,81.
Приложения:

Ответ дал:
0
Здравствуйте, можете помочь с алгеброй?
Похожие вопросы
1 год назад
2 года назад
9 лет назад