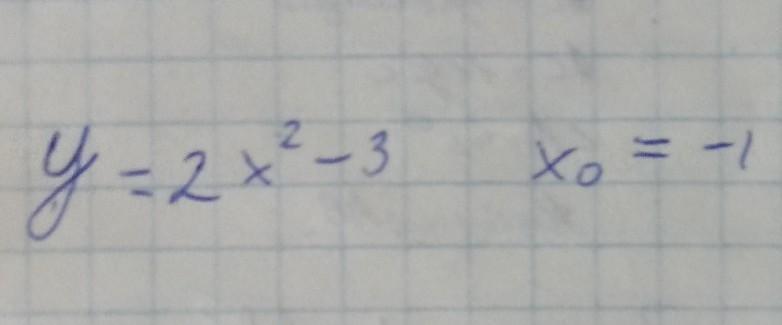Предмет: Математика
Автор: pickaboo
Вопрос задан 7 лет назад

< >

решите пример. уравнение косталеьное и нормальное

Приложения:

Ответы

Ответ дал: Correlation

0

Производная функции: $y'=(2x^2-3)'=4x$ .

Значение функции в точке $x_0=-1:~~ y(-1)=2cdot(-1)^2-3=-1$

Значение производной функции в точке $x_0=-1:~~ y'(-1)=4cdot(-1)=-4$

Уравнение касательной: $f(x)=y'(x_0)(x-x_0)+y(x_0)=-4(x+1)-1=-4x-4-1=boxed{-4x-5}$

Уравнение нормали: $g(x)=y_0-dfrac{1}{y'(x_0)}(x-x_0)=-1-dfrac{1}{-4}(x+1)=boxed{dfrac{x}{4}-dfrac{3}{4}}$

Похожие вопросы

Русский язык

1 год назад

Сколько раз в тексте на месте пропусков пишется буква И? Пр…бл…жа…тся пред…юньская пора. Каждый выпускник, готов…щ…йся к экзаменам, наде…тся на лучш…е. И хотя настроение скач…т и п…р…одически

Английский язык

1 год назад

complaints the disjunctive question

Русский язык

2 года назад

Составьте небольшой рассказ на русском языке,употребляя эти выражения. Забота о природе, законы природы, тайны природы, дары природы, природные ресурсы, охрана природы, охрана природы, охрана водных

Математика

2 года назад

ДОМАШНЕЕ ЗАДАНИЕ 9 Найди значения выражений, 208 . (50 820 : 33 + 460) : 40 (28 254:34 + 12 505:61) - 20 259 - 69 +1836:27

Алгебра

8 лет назад

Помогите: х4+2х2-3=0

Обществознание

8 лет назад

понятия финансовой грамотности

Геометрия

9 лет назад

Катеты прямоугольного треугольника равны 1 см и 75 см. Определите гипотенузу.

Литература

9 лет назад

Темой повести Ночь Перед рождеством является изображение... Пожалуйста помогите