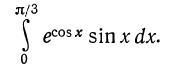Нужно решить с помощью подстановки.

Приложения:

Ответы

Ответ дал: takushnir

dcosx=-sinx*dx

-∫e^(cosx)d(cosx) пришли к табличному. ОН равен e^(cosx) верхний предел равен π/3, нижний 0, по Ньютону - Лейбницу

он равен -(е¹/²-е¹)=е-√е

2способ. Пусть соsx=в, тогда получим новые пределы интегрирования. Нижний предел 1, верхний предел 0.5.

-∫еᵇdв=-еᵇ; с учетом формулы Ньютона - Лейбница

получим -(е¹/²-е¹)=е-√е

Ответ дал: DagyBagy

Спасибо, Correlation показал более подробнее, т.к в этой теме я затупок.

Ответ дал: takushnir

))))))))))

Ответ дал: Correlation

$displaystyle intlimits^{frac{pi}{3}}_0e^{cos x}sin xdx=left{begin{array}{ccc}cos x=t\ \ -sin xdx=dtend{array}right}=-intlimits^{cosfrac{pi}{3}}_{cos0}e^tdt=\ \ \ =-intlimits^{frac{1}{2}}_1e^tdt=-e^tbigg|^{frac{1}{2}}_{1}=e-sqrt{e}$

Ответ дал: takushnir

по сути... это одно и то же. Я подставлял дифференциал от косинуса. а подведение под знак дифференциала - это всего лишь уловка выйти на табличный.

Ответ дал: Correlation

Большинство студентов, изучающие новую тему интегралы пока учат по табличным интегралам и каким-то подстановкам . Ну а потом уже показывают трюки. Я не возражаю показать второй способ. Лишь бы показать решение по требованию.

Похожие вопросы

Другие предметы

2 года назад

мои увлечения(секции,кружки) что можно здесь написать.это для портфолио.для мальчика 1 класс заранее спасибо...

Русский язык

2 года назад

Определи род имён существительных . За нашим посёлком темнеет большой еловый лес. Под елями всегда царит полумрак. Стоит запах хвои и сырости. Земля покрыта старыми хвоинками и лишайниками. На мягкой

История

2 года назад

Памажите пажалста даю 40 баллов. Что англичане считают началом своей свободы и почему?

Обществознание

2 года назад