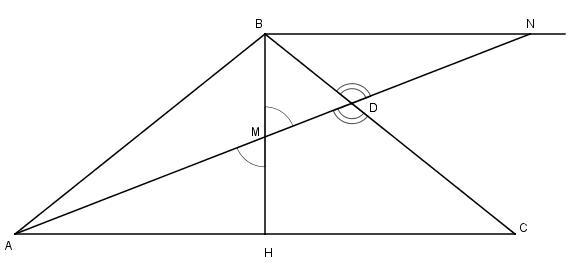
Дан ΔАВС равнобедренный, боковые стороны AB=BC. На стороне ВС взяли точку D, при этом BD : DC = 1 : 3. Нужно определить в каком отношении AD делит высоту BH ΔАВС, считая от вершины В.
Ответы
Ответ дал:
0
Пусть М — точка пересечения прямой AD и высоты BH. Через точку В проведём прямую, параллельную АС, и продолжим, AD до пересечения с это прямой в точке N. Пусть AH = CH = x, тогда AC = 2x.
Δ DBN ~ Δ CDA по двум углам, значит
Также ΔAMH и ΔBMN подобны по двум углам. Из подобия мы имеем
Ответ: 2 : 3.
Приложения:
Ответ дал:
0
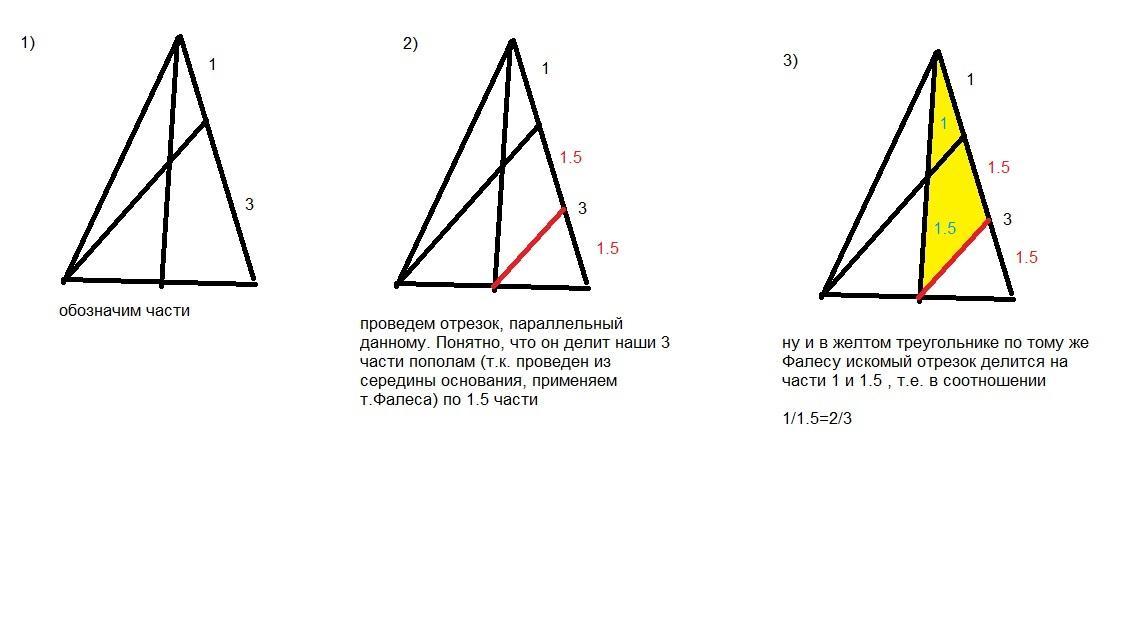
Ответ:Вот решение, как говорится, "на пальцах"
Объяснение:
Приложения:
Ответ дал:
0
Немного подробней решение записали бы.
Ответ дал:
0
так куда уж подробней - все там рассказано и разложено на элементарное.
Ответ дал:
0
ну вот вам подробней
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад