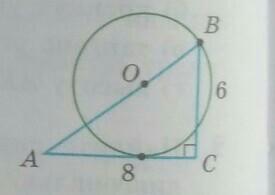
Окружность с центром О касается катета АС и проходит через вершину В прямоугольного треугольника АВС с катетами ВС=6, АС=8; точка О лежит на гипотенузе АВ(рис.). Найдите радиус этой окружности, используя определение синуса острого угла.
Приложения:
MrSolution:
без определения синуса можно до квадрата достроить в треугольнике, проведя 2 высоты из центра окружности и по отношению сторон, а затем и по телоеме Пифагора дать ответ. Так не подойдет?
или я не так понял чего?
не, не подойдёт
Ответы
Ответ дал:
7
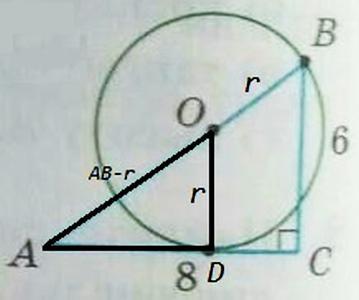
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
ABC - египетский треугольник, AB=10, sinA=BC/AB=3/5
Радиус OD перпендикулярен касательной AC.
sinA=OD/AO =r/(10-r) =3/5 <=> 10/r =8/3 <=> r=15/4
Приложения:
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад