• Предмет: Алгебра
  • Автор: nazariay
  • Вопрос задан 1 год назад
< >

Даны уравнения параболы и прямой .вычислить с помощью определенного интеграла площадь фигуры ,ограниченной данными линиями; сделать чертеж и заштриховать искомую площадь

Приложения:

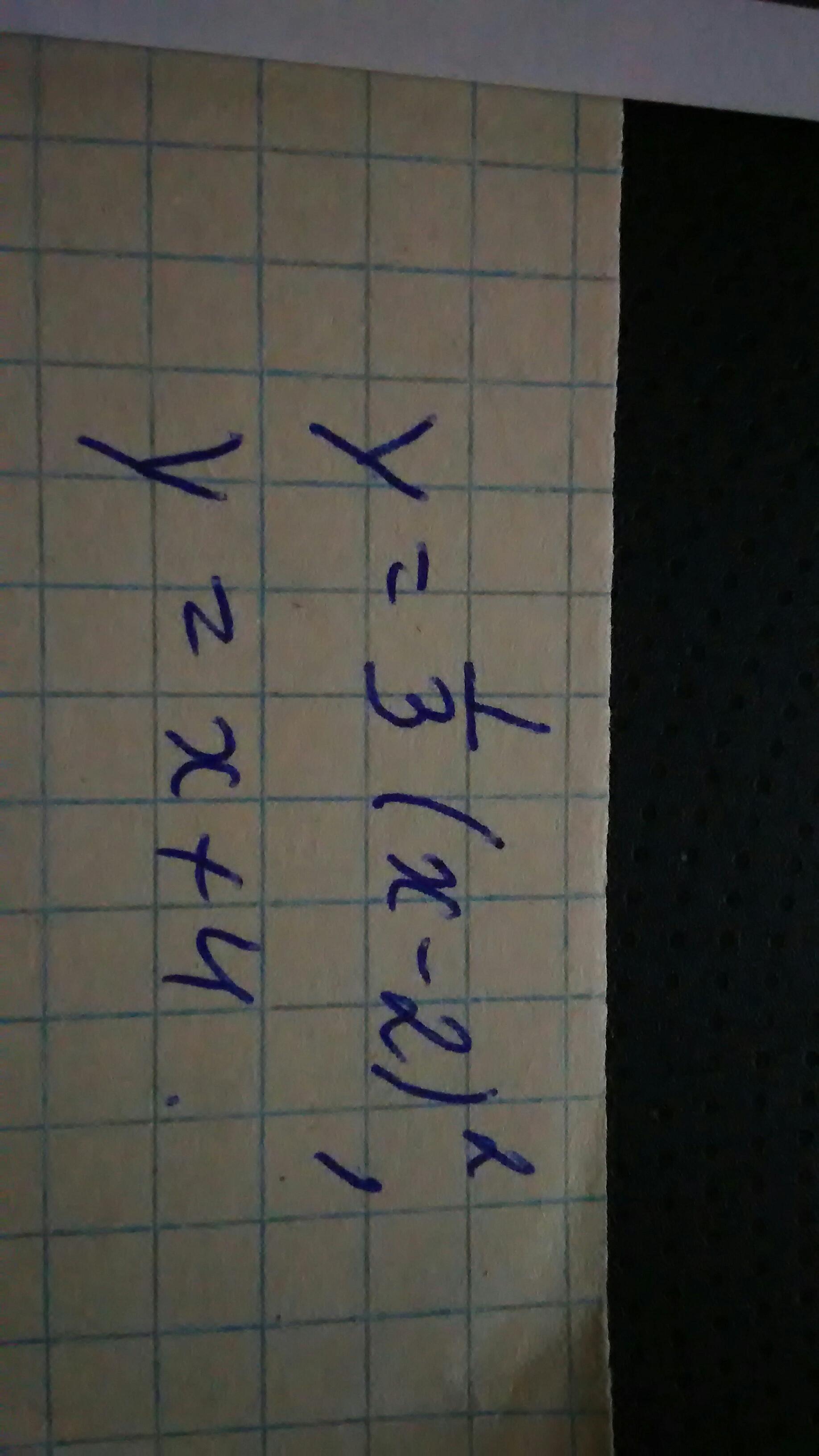
Ответы

Ответ дал: Аноним
1

S=\int\limits^8_{-1} (x+4-\frac{1}{3}(x-2)^2) } \, dx =(\frac{x^2}{2}+4x-\frac{1}{3} *\frac{(x-2)^3}{3})\ |^8_{-1}=\\ \\ =32+32-24-(\frac{1}{2}-4+3)=32+32-24-0.5+4-3=40.5

Приложения:
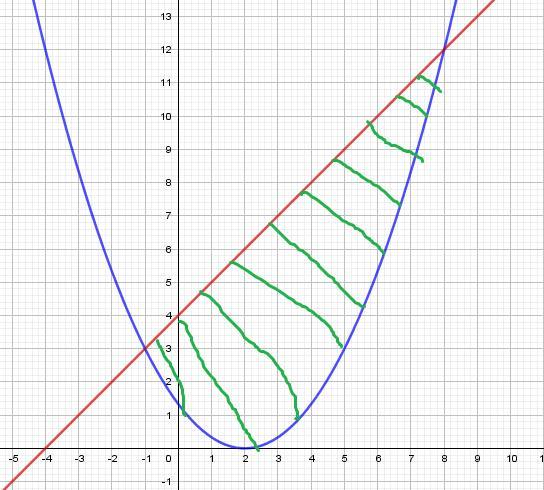
Ответ дал: NNNLLL54
2

y=\frac{1}{3}(x-2)^2\; \; ,\; \; y=x+4\\\\Tochki\; peresecheniya :\; \; \frac{1}{3}(x-2)^2=x+4\; ,\\\\\frac{1}{3}(x^2-4x+4)=x+4\; \; ,\; \; x^2-4x+4=3x+12\; ,\; \; x^2-7x-8=0\; ,\\\\x_1=-1\; ,\; \; x_2=8\; \; (teorema\; Vieta)\\\\S=\int\limits^8_{-1}\, \Big (x+4-\frac{1}{3}(x-2)^2\Big )\, dx=\Big (\frac{x^2}{2}+4x-\frac{1}{3}\cdot \frac{(x-2)^3}{3}\Big )\Big |_{-1}^8=\\\\=\frac{64}{2}+4\cdot 8-\frac{1}{3}\cdot \frac{6^3}{3}-\Big (\frac{1}{2}-4-\frac{1}{3}\cdot \frac{-27}{3}\Big )=\\\\=32+32-24-\frac{1}{2}+4-3=41-\frac{1}{2}=40,5

Приложения:
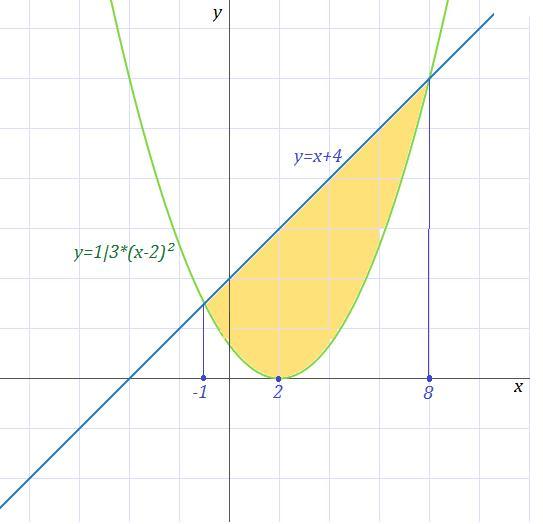
Похожие вопросы
Биология
1 год назад
Тема: Визначення реакції зіниць на світло. Мета: визначити реакцію зіниць на світло в людини. 1. Розгляньте зіниці в положенні, колі людина стоїть спиною до вікна. Визначте видимий розмір зіниць. 2.
География
1 год назад
Типи відтворення населення. Наведіть приклади країн.
Английский язык
1 год назад
пожалуйста помогите please ​
Английский язык
1 год назад
срочно срочно срочно помогите​
Окружающий мир
2 года назад
Выделение веществ из смеси Ученик исследует раствор, содержащий четыре компонента: воду, сахар, древесные опилки, гвозди. Он проводит разделение данной смеси поэтапно. Соотнеси этапы и действия.
Қазақ тiлi
2 года назад
Пожалуйста дам 50 баллов. Прошу срочно нужно :(​Шетелдік БАҚ - тың жазған мақалаларынан Астанада өткен экспо көрмесіне берілген оң бағаларын тауып , санамалап жаз . ( 4 ерекшеліктен артық табу керек )
Алгебра
8 лет назад
Решите неравенство ((2-x)(4x+3))/((x-3)^3(x+1)^2) <= 0
Алгебра
8 лет назад
ПОМОГИТЕ РЕШИТЬ УРАВНЕНИЕ