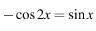Объясните, пожалуйста, как из этого получили sinx=1 и sinx=-1/2

правая часть: косинус двойного угла

====================================

cos(2α)=cos2(α)−sin2(α)

cos(2α)= 1−2·sin2(α)

cos(2α)= 2·cos2(α)−1

===================

-cos²х+sin²х=sinx

-(1-sin²x)+sin²x=sinx

-1+sin²x+sin²x-sinx=0

2sin²x-sinx-1=0

==============

замена: sinx=t

2t²-t-1=0

D=1²-4*2*(-1)=9

√D=3

x1=(1-3)/4=-1/2

x2=1

=====

возвращаемся к замене:

sinx=1

sinx=-1/2

==========