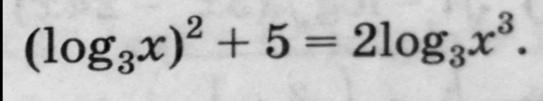Предмет: Алгебра
Автор: ClarisVerbis
Вопрос задан 1 год назад

Требуется решить уравнения.

Приложения:

Ответы

Ответ дал: NNNLLL54

Объяснение:

$(log_3x)^2+5=2\, log_3x^3\; \; ,\; \; \; \; ODZ:\; x>0\; ,\\\\(log_3x)^2-6\, log_3x+5=0\\\\log_3x=1\; \; \; \; ili\; \; \; \; log_3x=5\; \; \; \; (teorema\; Vieta)\\\\x=3\qquad ili\qquad x=3^5\\\\Otvet:\; \; x=3\; ,\; \; x=243\; .$

Ответ дал: Аноним

Введем замену ㏒₃х=у, где х>0, тогда у²-6у+5=0.

По теореме, обратной теореме Виета, у₁=1, у₂=5, вернемся к старой переменной х.

㏒₃х=1⇒х=3

㏒₃х=5⇒х=3⁵=81*3=243

Оба корня входят в ОДЗ

Ответ 3; 243

Похожие вопросы

Английский язык

1 год назад

1. What is the greatest achievement of human genius? 2 When do we celebrate Radio Day? 3. What did Popov demonstrate to a meeting of the Russian Physical and Chemistry Society? 4. When was Popov

Математика

1 год назад

Допоможіть будь ласка!!! ДАЮ 30 БАЛЛІВ!! ФОТО НИЖЧЕ⬇️⬇️

Алгебра

1 год назад

Решите систему уравнений , помогите мне пожалуйста а то не понимаю!!! Заранее благодарен

Математика

1 год назад

В первый день продали 40% всех роз, во второй 60% остального, а в третий - оставшиеся 72 розы. Сколько всего роз продано за три дня?

Литература

2 года назад

Составить план Не везёт,В.Голявкин

Алгебра

2 года назад

возведите данное выражение в степень:(3x)^6

Алгебра

8 лет назад

За 41 ч по течению реки теплоход проходит тот же путь, что за 43 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч. Ответ: скорость теплохода км/ч.

Информатика

8 лет назад

Пожалуйста помогите, надо сдавать работу ! Написать программу на языке С++ В заданном одномерном массиве поменять местами соседние элементы, стоящие на чётных местах, с элементами, стоящими на