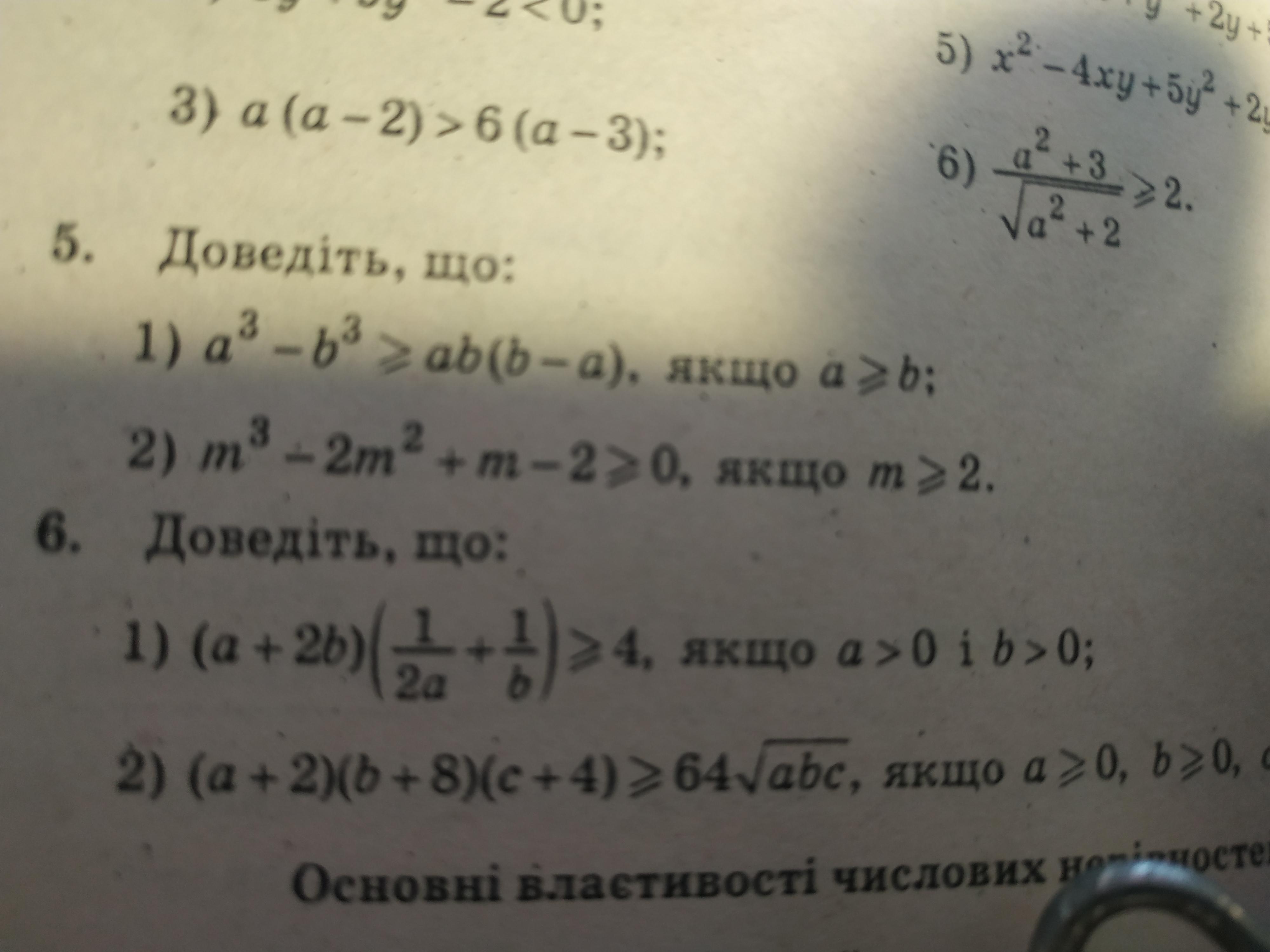• Предмет: Алгебра
  • Автор: katyapuh
  • Вопрос задан 1 год назад
< >

Доказать, что (a+2b)(1/2a + 1/b) больше или равно 4
Если a>0 и b>0

Приложения:

Ответы

Ответ дал: Аноним
3

По неравенству Коши

a+2b\geqslant 2\sqrt{a}\cdot \sqrt{2b}=2\sqrt{2ab}\\ \\ \dfrac{1}{2a}+\dfrac{1}{b}\geqslant2\sqrt{\dfrac{1}{2a}}\cdot \sqrt{\dfrac{1}{b}}=2\sqrt{\dfrac{1}{2ab}}

Умножив эти два неравенства, получим

(a+2b)\left(\dfrac{1}{2a}+\dfrac{1}{b}\right)\geqslant 2\sqrt{2ab}\cdot \dfrac{2}{\sqrt{2ab}}=4

Доказано.

Похожие вопросы
Русский язык
1 год назад
Спишите предложения, изменяя слова в скобках. Рыбак поймал огромного (лещ). Увидел (грач) — весну встречай Птенцы грелись под тёплыми (луч) солнца. к больному позвали (врач). Выручай (товарищ)
Алгебра
1 год назад
3 и 4 помогите пожалуйста даю 55 балов
Другие предметы
1 год назад
Що допомогло Бубі залишитися собою? а) улюблені книжки б)дідусева іронія в)хороші фільми ​
Українська мова
1 год назад
Допоможiть срочннооо
Математика
2 года назад
пожалуйста помогите мне пожалуйста срочно дам 100 балов и можно пожалуйста с решением пожалуйста​
Физика
2 года назад
От капли воды с электрическим зарядом -2q отделили каплю зарядом 2q. Определите заряд оставшейся капли. Срочно даю 50 балов ​
Математика
8 лет назад
Урок продолжается 3/4 часа перемена 1/6 часа Сколько времени продолжались два урока и две перемены Please пожалуйста помогите!!!!!
Математика
8 лет назад
Выполните сложение 5) -1/4+(-1/2) 6) -3целых 4/5+2 целых 2/3