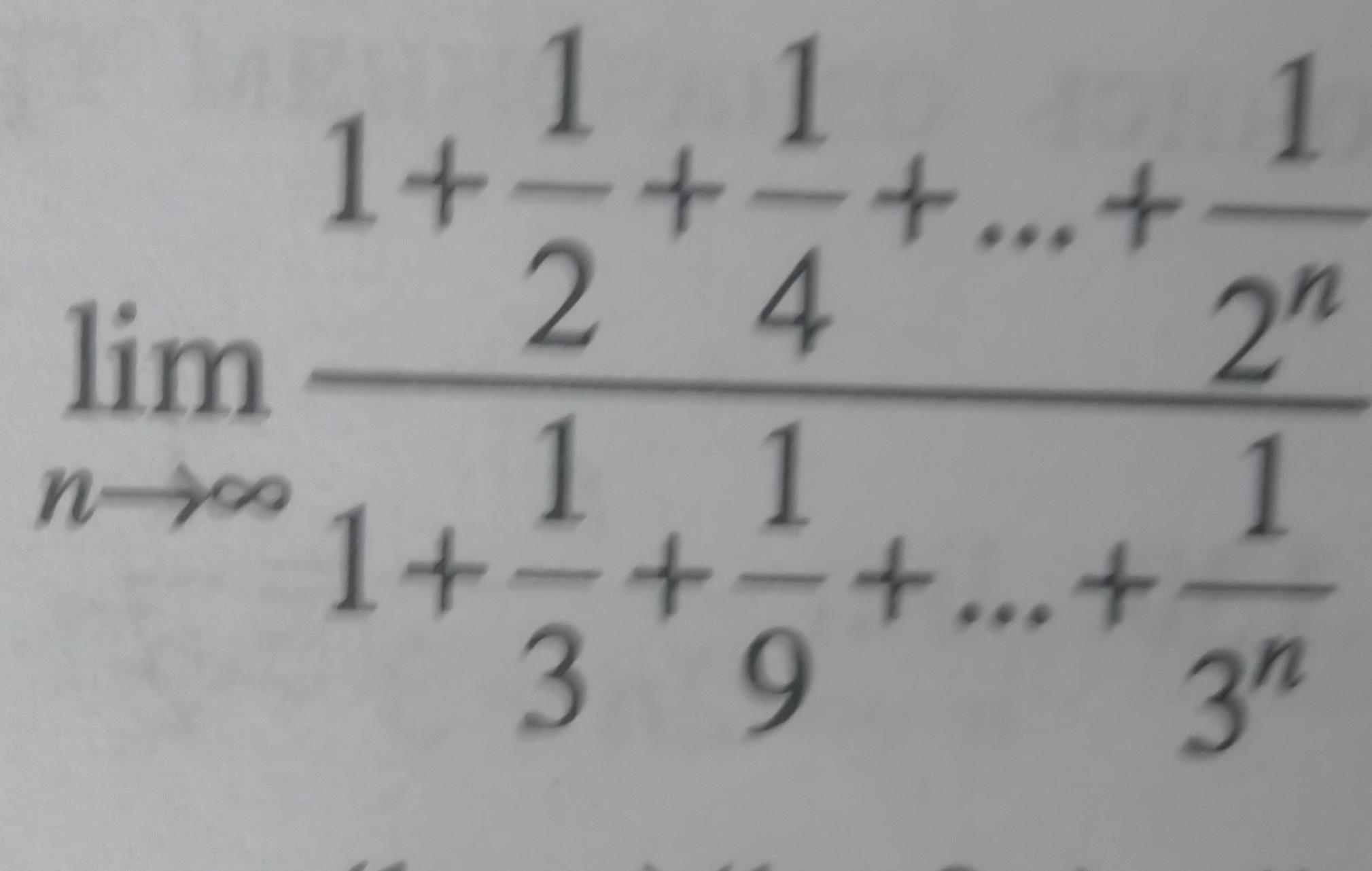Предмет: Алгебра
Автор: bertain
Вопрос задан 1 год назад

< >

70б + лучший ответ! Найти предел функции (с подробным объяснением):

Приложения:

Ответы

Ответ дал: Аноним

1

Последовательности стоящие в числителе и в знаменателе являются геометрической прогрессией с первым членом 1; знаменателем 0,5 и с первым членом 1; знаменателем 1/3, соответственно.

Найдем их сумму первых n членов

$\displaystyle \lim_{n \to \infty}\frac{1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^n}}{1+\dfrac{1}{3}+\dfrac{1}{9}+...+\dfrac{1}{3^n}}=\lim_{n \to \infty}\dfrac{\dfrac{1-\dfrac{1}{2^n}}{1-\dfrac{1}{2}}}{\dfrac{1-\dfrac{1}{3^n}}{1-\dfrac{1}{3}}}=\dfrac{4}{3}\lim_{n \to \infty}\dfrac{1-\dfrac{1}{2^n}}{1-\dfrac{1}{3^n}}=\dfrac{4}{3}$

bertain: Большое спасибо! :)

Аноним: На здоровье ! :)

Ответ дал: Аноним

2

Ответ и решение во вложении

Приложения:

aleksoref: Здравствуйте, помогите пожалуйста
https://znanija.com/task/32908181

Похожие вопросы

Химия

1 год назад

Напишіть рівняння реакцій, користуючись схемами та вкажи реакції розкладу та сполучення: а) КСЮО3 - ? + ?; 6) Fe + O2 → ?; B) KMnO4 - ? + ? + O2 г) K + O2 → ? д) Н2О2- Н2О + ? ДОПОМОЖІТЬ

Английский язык

1 год назад

They into this house in 2014. O have moved O did move Omoved

Русский язык

1 год назад

Укажите предложение с последовательным

Английский язык

1 год назад

Помогите пожалуйста... очень прошу, заранее спасибо!:)

Русский язык

2 года назад

Кто сдесь самый умный помогите пжл!)))

Қазақ тiлi

2 года назад

32-жаттығу Меңзер бағыты бойынша бір әріп тастай отырып , мақал құрастырып оқы. Кім біледі жауабын. Көмек керек.

Математика

8 лет назад

Из 28 кг хлопкового семени получили 7 кг масла. Найди, сколько масла получится из 14 кг хлопкового семени. помогите пжл

Математика

8 лет назад

Упростить выражение 328+n+482 378-(k+258) Кратко