100 баллов! Построить график.
y=3^log3(x^2 - 4x + 3)
Логорифма в степени.

Ответы

Ответ дал: Аноним

Решение и ответ во вложении

Приложения:

VAlDEROR: спасибо!

Аноним: спасибо)

Ответ дал: Аноним

Функция существует, когда под логарифмическое выражение положительно, т.е.

$x^2-4x+3>0\\ x^2-4x+4-1>0\\ (x-2)^2>1\\ |x-2|>1\\ \left[\begin{array}{ccc}x-2>1\\ \\ x-2<-1\end{array}\right~~~\Rightarrow~~~\left[\begin{array}{ccc}x>3\\ \\ x<1\end{array}\right$

Упростим функцию

$y=3^{\log_3(x^2-4x+3)}=x^2-4x+3$

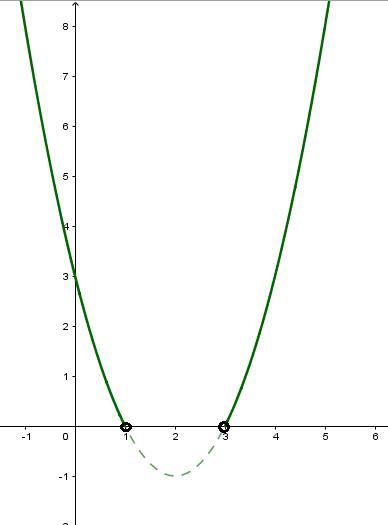
Графиком функции есть парабола, ветви которой направлены вверх. Найдем ее координаты вершины параболы

$m=-\dfrac{b}{2a}=\dfrac{4}{2}=2\\ \\ y=2^2-4\cdot 2+3=-1$

Координаты вершины параболы (2;-1)

Приложения:

Похожие вопросы

Математика

1 год назад

№1. Відстань між двома містами на карті дорівнює 12 см. Яка відстань між цими містами на місцевості, якщо масштаб карти 1 : 600 000? №2. Відстань між двома селами на місцевості дорівнює 5,6 км. Яка

География

1 год назад

Частина географічного поясу з однорідними кліматичними умовами?

Другие предметы

1 год назад

чи може Буратіно довіряти карабас-барабас

Русский язык

1 год назад

объясните фразеологизмы В ступе воду не толочь Через сугроб, через ухаб Держать в чёрном теле Не снимай уздысорвать последнюю рубашку СРОЧНОО

Другие предметы

2 года назад

Выполнить разрез детали

Английский язык

2 года назад

помогите пожалуйста

Физика

8 лет назад

в каких системах отсчёта не выполняется второй закон Ньютона?

Математика

8 лет назад

Используя основное свойство дроби найди значение x : 1) 4x +1/11 = 50/22; 3) 72/60= 18/4x+7

100 баллов! Построить график.y=3^log3(x^2 - 4x + 3)Логорифма в степени.​

Ответы

100 баллов! Построить график.
y=3^log3(x^2 - 4x + 3)
Логорифма в степени.