Предмет: Алгебра
Автор: Алкадиеныч
Вопрос задан 1 год назад

< >

Найти сумму ряда
$qsina+q^2sin2a+...+q^nsinna+...$

igorShap: Q любое, или есть ограничение?

Алкадиеныч: для этого примера нету ограничений на q

Алкадиеныч: https://sun9-49.userapi.com/c857636/v857636496/95adc/1j6IGl3LdGc.jpg

igorShap: Ну, видимо авторы сборника подразумевали это замечание к обоим примерам, потому что в случае |q|>=1 сходимость не гарантирована. У нас ведь будет nый член равен произведению бесконечно большого числа на член ограниченной последовательности.

igorShap: Только опечатка, |q|>1, для 1 недавно уже была задача Вами предложена

Аноним: Задача с конспекта :D На комплексном анализе была..

Аноним: Но не составит труда самому решить. Задача легкая

Алкадиеныч: Оч легкая:)

Ответы

Ответ дал: Аноним

1

$q\sin \alpha+q^2\sin2\alpha+...+q^n\sin n\alpha+...$

$q\cos \alpha+q^2\cos2\alpha+...+q^n\cos n\alpha+...$ , |q|<1

Пусть $b_n$ и $a_n$ - последовательности частичных сумм первого и второго, соответственного и b , a - их суммы.

По формуле Эйлера $e^{i\phi}=\cos \phi +i\sin \phi$ , мы получим

$b_n+ia_n=qe^{i\alpha}+q^2e^{2i\alpha}+...+q^ne^{ni\alpha}+...=\dfrac{qe^{i\alpha}}{1-qe^{i\alpha}}~~\boxed{=}$

Здесь в этом случае бесконечно убывающая геометрическая прогрессия.

Преобразовывая в тригонометрическую форму по формуле Эйлера, мы получим

$\boxed{=}~q\left(\dfrac{\cos\alpha -q}{1-2q\cos\alpha+q^2}+i\dfrac{q\sin\alpha}{1-2q\cos\alpha+q^2}\right)$

Откуда искомая сумма ряда $b=q\cdot\dfrac{\cos\alpha -q}{1-2q\cos\alpha+q^2}$

Приложения:

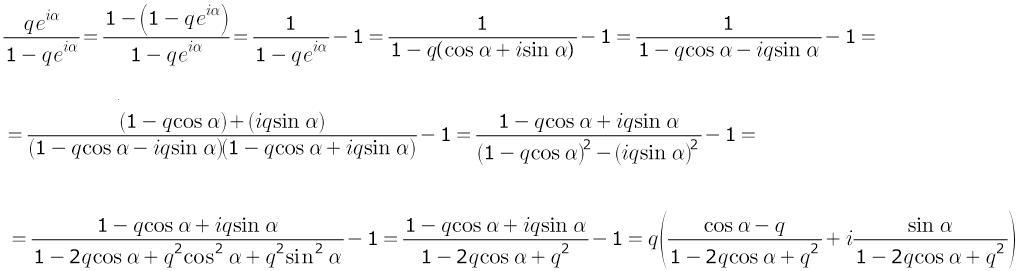
Аноним: Добавил вычисления в фотке

Похожие вопросы

Физика

1 год назад

Електричний нагрівник за час, що дорівнює 5 хв, доводить до кипіння 5 кг води, початкова температура якої 25 °С. Якою є сила струму в нагрівальному елементі, якщо напруга в мережі становить 220 В?

Химия

1 год назад

Встановіть відповідність між формулами гідратів та назвами оксидів, що їх утворюють у результаті реакцій сполучення з водою. 1.Са(ОН)2 а.калій оксид 2.KOH б.сульфур(VI) оксид 3.H2SO4 в.кальцій

Английский язык

1 год назад

Выберете правильный вариант срочно надо пожалуйста :) The bag is not … for me to buy. * 1)too cheap 2)enough cheap 3)cheap enough 4)cheap too

Биология

1 год назад

- - - xxxxxxxx, Толсоси, та 4. . Укажіть отруйний шапковий гриб. А –боровик; В- мукор; С- мухомор; D- пеніциліум.

Немецкий язык

2 года назад

Aufgabe 1. Setze das Verb haben richtig ein. hat-hatben- Hast - hat-habe-hat 1..........du die kleine Hexe gehen? 2. Des..........mein Freund gesngt. 3. Die Stunde.......... 45 Minuten gedauert. 4

Алгебра

2 года назад

Это верное свойство?

Биология

8 лет назад

Нервную систему по месту расположения условно разделяют на ??? СРОЧНОО

Математика

8 лет назад

сколько будет 2х2? п.с 20 баллов