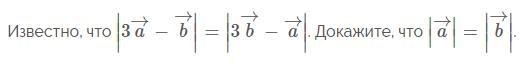Условие и вопрос предоставлен на рисунке

Приложения:

Ответы

Ответ дал: Andr1806

Ответ:

Доказательство в объяснении.

Объяснение:

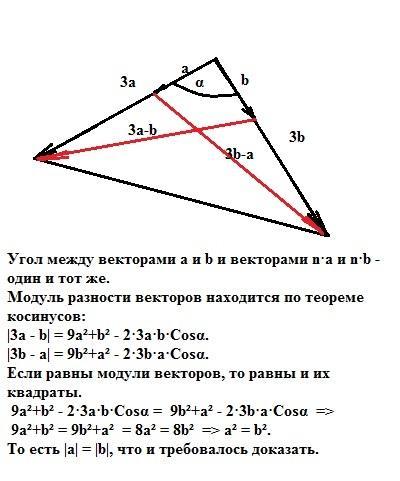
Угол между векторами а и b и векторами n·a и n·b - один и тот же.

Модуль разности векторов находится по теореме косинусов:

|3a - b| = 9a²+b² - 2·3a·b·Cosα.

|3b - a| = 9b²+a² - 2·3b·a·Cosα.

Если равны модули векторов, то равны и их квадраты.

9a²+b² - 2·3a·b·Cosα = 9b²+a² - 2·3b·a·Cosα =>

9a²+b² = 9b²+a² = 8a² = 8b² => a² = b².

То есть |a| = |b|, что и требовалось доказать.

Приложения:

Аноним: Ну можно так )

Ответ дал: Аноним

Левую и правую частей равенства можно представить в виде

$\sqrt{\Big(3\vec{a}-\vec{b}\Big)^2}=\sqrt{\Big(3\vec{b}-\vec{a}\Big)^2}\\ \\ \\ \Big(3\vec{a}-\vec{b}\Big)^2=\Big(3\vec{b}-\vec{a}\Big)^2\\ \\ 9\vec{a}\vec{a}-6\vec{a}\cdot\vec{b}+\vec{b}\vec{b}=9\vec{b}\vec{b}-6\vec{a}\cdot\vec{b}+\vec{a}\vec{a}\\ \\9\vec{a}^2+\vec{b}^2=9\vec{b}^2+\vec{a}^2\\ \\ 9\vec{a}^2-\vec{a}^2=9\vec{b}^2-\vec{b}^2\\ \\ 8\vec{a}^2=8\vec{b}^2\\ \\ \vec{a}^2=\vec{b}^2~~~\Rightarrow~~~\Big|\vec{a}\Big|=\Big|\vec{b}\Big|$