В треугольнике ABC медиана ВМ перпендикулярна биссектрисе АР найдите угол АВС если известно что угол ВАР =30 градусов
Ответы
Ответ дал:
2
Ответ:
∠АВС = 90°.
Объяснение:
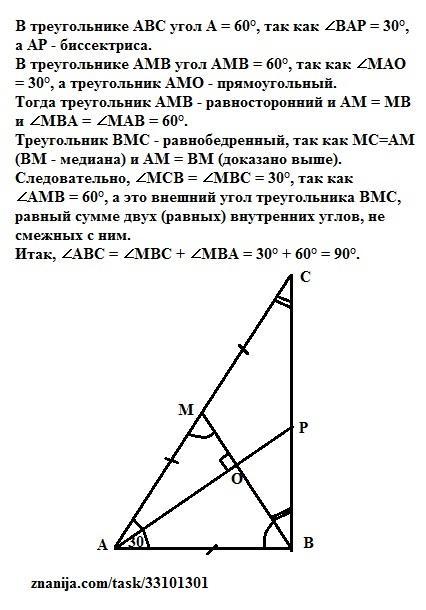
В треугольнике АВС угол А = 60°, так как ∠ВАР = 30°, а
АР - биссектриса.
В треугольнике АМВ угол АМВ = 60°, так как ∠МАО = 30°, а треугольник АМО - прямоугольный.
Тогда треугольник АМВ - равносторонний и АМ = МВ и
∠МВА = ∠МАВ = 60°.
Треугольник ВМС - равнобедренный, так как МС=АМ (ВМ - медиана) и АМ = ВМ (доказано выше). Следовательно, ∠МСВ = ∠МВС = 30°, так как ∠АМВ = 60°, а это внешний угол треугольника ВМС, равный сумме двух (равных) внутренних углов, не смежных с ним.
Итак, ∠АВС = ∠МВС + ∠МВА = 30° + 60° = 90°.
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад