ПОЖАЛУЙСТА ПОМГИТЕ.29 БАЛОВ


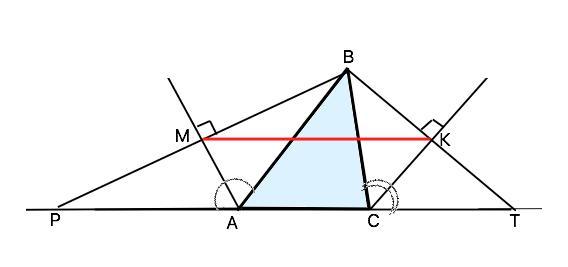
Кути BAD і BCE – зовнішні кути трикутника ABC. Із вершини B проведено перпендикуляри BM і BK до бісектрис кутів BAD і BCE відповідно. Знайдіть відрізок MK, якщо периметр трикутника ABC дорівнює 10 см.

Ответ: 5 см

Объяснение:

     Углы ВАD  и ВСЕ - внешние углы треугольника АВС.  Из вершины В проведены перпендикуляры ВМ и ВК к биссектрисам углов ВАD и все соответственно. Найти отрезок МК, если периметр треугольника АВС равен 10 см

              *    *    *

 Продолжим ВМ и ВК до пересечения в т.Р и т.Т с прямой, содержащей сторону АС. В треугольнике РАВ  отрезок АМ  биссектриса угла РАВ, угол РМА=ВМА=90°.  Треугольники РАМ и ВАМ равны по двум углам, прилежащим к общей стороне АМ. Следовательно, РА=АВ и РМ=МВ ( точка М - середина РВ).

Аналогично в ∆ ВСТ ВК=ТК и СТ=ВС, а точка К - середина ВТ.  Отрезок МК - средняя линия ∆ РВТ.

Поэтому РА+АС+СТ=ВА+АС+ВС=периметр АВС.  МК=Р(АВС):2=10:2=5 см