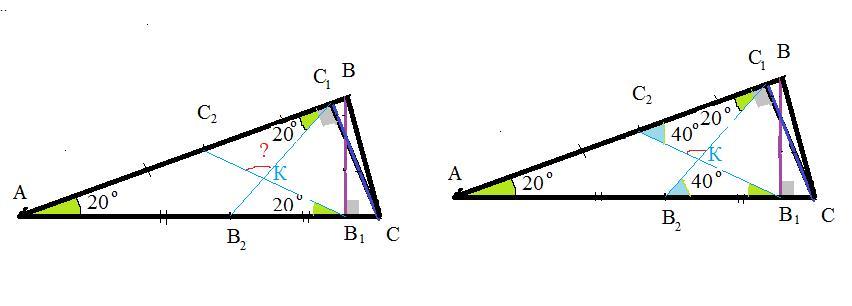
В остроугольном треугольнике ABC угол A равен 20∘, отрезки BB1 и CC1 — высоты, точки B2 и C2 — середины сторон AC и AB соответственно. Прямые B1C2 и C1B2 пересекаются в точке K. Найдите величину (в градусах) угла C1KC2.

∠ВАС=20°

В прямоугольном треугольнике  АСС₁

С₁В₂ -медиана .

Значит, АВ₂=С₁В₂=В₂С

Треугольник  АВ₂С₁ -  равнобедренный.

∠ВАС=∠АС₁В₂=20°

Аналогично

В прямоугольном треугольнике  АВВ₁

В₁С₂ -медиана.

Значит, АС₂=С₂В₁= С₂В

Треугольник  АВВ₁ -  равнобедренный.

∠ВАС=∠АВ₁С₂=20°

∠С₁В₂С=40°  - внешний угол треугольника равен сумме внутренних с ним не смежных

Тогда ∠С₁КС₂=180°-20°-40°=120°