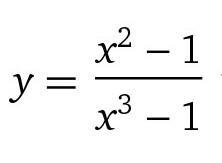• Предмет: Алгебра
  • Автор: вкпа
  • Вопрос задан 1 год назад
< >

15 БАЛЛОВ. исследовать функцию на непрерывность и описать точки разрыва​

Приложения:

Ответы

Ответ дал: Аноним
2

Разрыв функции будет в точке x = 1

\displaystyle \lim_{x \to 1\pm0}\frac{x^2-1}{x^3-1}=\lim_{x \to 1\pm0}\frac{(x-1)(x+1)}{(x-1)(x^2+x+1)}=\lim_{x \to 1\pm0}\frac{x+1}{x^2+x+1}=\frac{2}{3}

Поскольку односторонние пределы равны, то данная функция непрерывна в точке x = 1 и функция имеет точку разрыва первого рода.

LSM54: Помогите,пожалуйста! https://znanija.com/task/33209454 https://znanija.com/task/33210304
sisgghhhhi: https://znanija.com/task/33210772
sisgghhhhi: на логику пж) 2 это невер
sisgghhhhi: неверно
Похожие вопросы
Қазақ тiлi
1 год назад
Помогите составить 4 предложения об Алматы корыгы на казахском языке СРОЧНОООО!!¡¡¡¡!!!!! ДО ЗАВТРАААА ​
Физика
1 год назад
допоможіть будь ласка ​
Геометрия
1 год назад
5. За допомогою транспортира накресліть кут, градусна міра якого дорівнює 70°, та проведіть його бісектрису.​
Математика
1 год назад
Как решить 1000-(468+254) в столбик?
Обществознание
2 года назад
зачем человеку трудится?
Русский язык
2 года назад
1. Вставьте пропущенные буквы. Сидел пр…спокойно, пр…красная музыка, пр…глушить свет, пр…задуматься над проблемой, колючая пр…града, пр…чалить к берегу, пр…школьный участок, пр..чина, пр..ключение,
Математика
8 лет назад
Составь примеры и запиши их.
Литература
8 лет назад
Сочинени по картине «Взятие снежного городка» В. И. Суриков Пж очень нужно