Предмет: Геометрия
Автор: Мозговина12
Вопрос задан 1 год назад

П_О_М_О_Г_И_Т_Е_ ♥♥♥ П_О_Ж_А__Л_У_Й_С_Т_А)))

❖❖❖ ❖❖❖ ❖❖❖ ❖❖❖ ❖❖❖ ❖❖❖ ❖❖❖ ❖❖❖

Составить общие уравнения прямой, образованной пересечением плоскости

х +2y-z+5 =0 с плоскостью , проходящей через ось Оу и точку М(5, 3, 2).

Приложения:

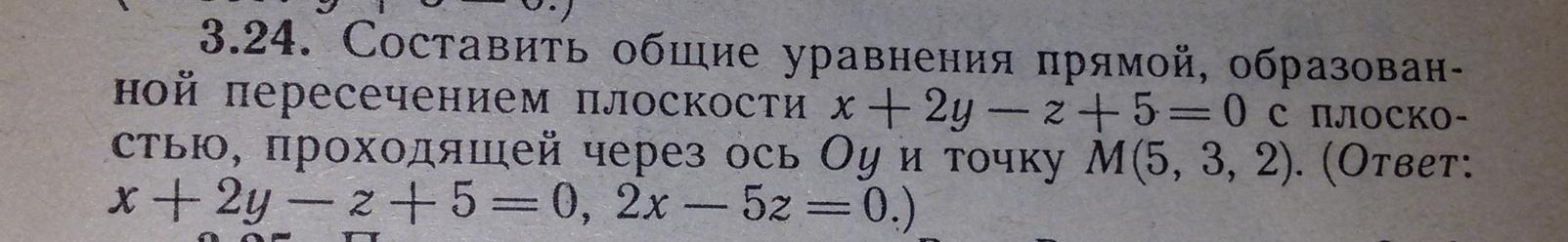
Ответы

Ответ дал: NNNLLL54

Cоставим сначала уравнение плоскости, проходящей через ось ОУ и точку М(5,3,2).

Так как ось ОУ принадлежит искомой плоскости α, то любая точка, лежащая на оси ОУ, принадлежит плоскости α . В том числе и начало координат, точка О(0,0,0) ∈α .

Так как точка М(5,3,2)∈α , то и вектор ОМ∈α . Координаты вектора ОМ=(5,3,2) .

Также единичный вектор оси ОУ, вектор j=(0,1,0) , принадлежит плоскости α .

Можем записать нормальный вектор искомой плоскости α как векторное произведение векторов ОМ и j .

$\vec{n}=\Big [\, \overline {OM}\, ,\; \vec{j}\, \Big ]=\left|\begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\5&3&2\\0&1&0\end{array}\right|=-2\vec{i}+5\vec{k}\\\\\\\lambda =-1\; \; \Rightarrow \; \; \; \; \vec{n}_1=\lambda \vec{n}=(2,0,-5)\\\\\alpha :\; \; A(x-x_0)+B(y-y_0)+C(z-z_0)=0\\\\2\cdot (x-5)+0\cdot (y-3)-5\cdot (z-2)=0\\\\\boxed {\alpha :\; \; 2x-5z=0}$