Предмет: Математика
Автор: Аноним
Вопрос задан 1 год назад

< >

Вычислить неопределенный интеграл методом интегрирования по частям, формула дана ниже:

$\int\limits {u} \, dv=uv-\int\limits {v} \, du$

Приложения:

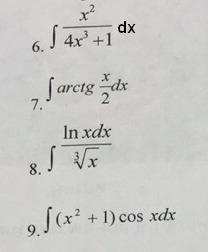
Ответы

Ответ дал: axatar

1

Ответ:

Ответы в объяснении

Пошаговое объяснение:

6. $\int\limits {\frac{x^{2} }{4x^{3}+1} } \, dx=$

$=\int\limits {\frac{1 }{4x^{3}+1} } \, d(\frac{x^{3}}{3} )=$

$=\frac{1}{3*4} \int\limits {\frac{1 }{x^{3}+\frac{1}{4} } } \, d(x^{3}+\frac{1}{4} ) =$

$=\frac{1}{12} ln|x^{3}+\frac{1}{4}|+c$

7. $\int\limits {arctg\frac{x}{2} } \, dx=[u=arctg\frac{x}{2}, du=\frac{4dx}{x^{2} +2^{2}}, dv=dx, v=x]=$

$=arctg\frac{x}{2}*x-\int\limits {x*\frac{4}{x^{2} +2^{2}}} \, dx=$

$=arctg\frac{x}{2}*x-4*\int\limits {\frac{1}{x^{2} +2^{2}}} \, d(\frac{x^{2}}{2}) =$

$=arctg\frac{x}{2}*x-2*\int\limits {\frac{1}{x^{2} +2^{2}}} \, d(x^{2}+2^{2}) =$

$=arctg\frac{x}{2}*x-2*ln(x^{2} +2^{2})+c$

8. $\int\limits {\frac{lnx}{\sqrt[3]{x} } } \, dx=[u=lnx, du=\frac{1}{x}dx, dv=\frac{1}{\sqrt[3]{x} } dx, v=\frac{3}{2} \sqrt[3]{x^{2} } }]=$

$=lnx*\frac{3}{2} \sqrt[3]{x^{2} } }-\int\limits {\frac{3}{2} \sqrt[3]{x^{2} } }*\frac{1}{x} } \, dx=$

$=\frac{3}{2} \sqrt[3]{x^{2} } }*lnx-\frac{3}{2}\int\limits {\frac{1}{\sqrt[3]{x} }} } \, dx=$

$=\frac{3}{2} \sqrt[3]{x^{2} } }*lnx-\frac{3}{2}*\frac{3}{2} *\sqrt[3]{x^{2} } }+c=$

$=\frac{3}{2} \sqrt[3]{x^{2} } }*(lnx-\frac{3}{2})+c$

9. $\int\limits {(x^{2}+1 )cosx } \, dx=[u=x^{2}+1, du=2xdx, dv=cosxdx, v=sinx]=$

$=(x^{2}+1 )sinx-\int\limits {sinx*2x} \, dx=(x^{2}+1 )sinx-2*\int\limits {x*sinx} \, dx=$

$=[u=x, du=dx, dv=sinxdx, v=-cosx]=(x^{2}+1 )sinx-2*(x*(-cosx)-\int\limits {(-cosx)} \, dx)=$

$=(x^{2}+1 )sinx-2*(x*(-cosx)+sinx))+c=(x^{2}+1 )sinx+2*x*cosx-sinx+c=$

$=x^{2}*sinx+2*x*cosx+c$

Аноним: Благодарю!

axatar: Рад помочь

Похожие вопросы

Математика

1 год назад

Помогите пожалуйста 8. Зобразіть на координатній площині множину точок, що задовольняють умовам:

Информатика

1 год назад

Задания 2. Заполни пропуски: Дан код программы нахождения. площади треугольника: h=float( a=float( s=1/2*a*th 5 (s) (2 балла) и треугольника, вставьте пропущенные ("задайте значение в соты

Математика

1 год назад

Можешь решить .Вычислите: (- 4, 6) + (- 1 3/14) пожалуйста! Срочно! Полным решением!

Математика

1 год назад

Знайди добуток скоротивши його 3/19*17/3

Другие предметы

2 года назад

что такое выкройка?

Биология

2 года назад

Узнайте, какой еще существует тип автотрофного питания, помимо фотосинтеза. Для каких организмов он характерен? По какой причине они используют не фотосинтез, а другой тип автотрофного питания? 68 б

Математика

8 лет назад

помогите пожалуйста! 509

Математика

8 лет назад

ПЖ СРОЧНО ПОМОГИТЕ На игральном кубике записаны числа от 1 до 6. Вася 5 раз бросал кубики и получил при первом броске сумму 17, при втором 19, потом 20, 21 и 26. Ни на одном из кубиков одна грань не