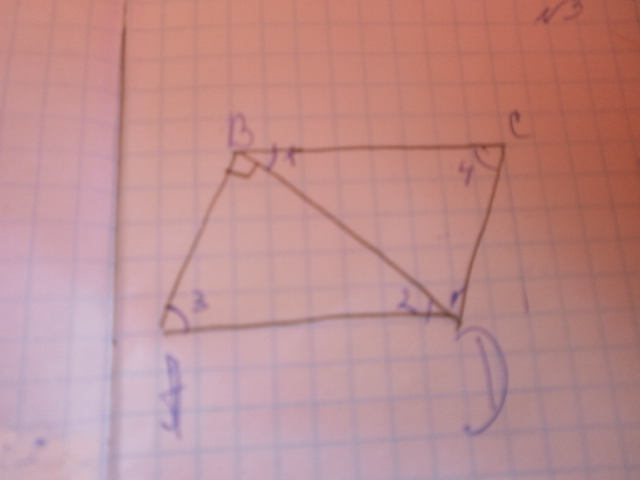
ABCD параллелограмм BD диагональ и биссиктриса= половине AD,найти углы параллелограмма.

BD  это диагональ и биссектриса. Значит треугольники ABD и BCD равнобедренные и АВ=AD, а BC=CD.Тогда ABCD - ромб, так как ромб это параллелограмм, у которого все стороны равны.Диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам.
У нас BD= 0,5AD. Значит синус угла CAD = 0,25AD/AD = 0,25. Угол CAD ≈ 15°.
То есть угол А равен 30°, а угол В равен 150°(так как углы, прилежащие к одной стороне параллелограмма равны в сумме 180°)
Итак углы ABCD равны <A=<C = 30°; <B=<D = 150°