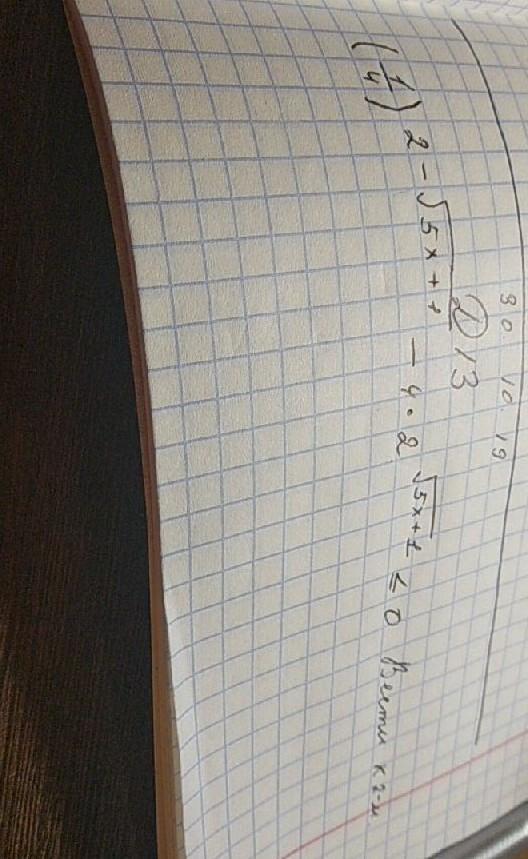• Предмет: Математика
  • Автор: Аноним
  • Вопрос задан 1 год назад
< >

(1/4)^2-√5x+1- 4*2^√5x+1<0 вести нужно те 2 срочно нужно решить ​

Приложения:

Ответы

Ответ дал: yakfedor
1

Ответ:

x \leq  7

Пошаговое объяснение:

(\frac{1}{4}) ^{2-\sqrt{5x+1} } -4*2^{\sqrt{5x+1} }\leq  0

4 ^{\sqrt{5x+1}-2 } -2^{2} *2^{\sqrt{5x+1} }\leq  0

2 ^{2*(\sqrt{5x+1}-2) } -2^{2} *2^{\sqrt{5x+1} }\leq  0

2 ^{2*\sqrt{5x+1}-4 } \leq  2^{\sqrt{5x+1} +2}

теперь можно сравнить степени

2*\sqrt{5x+1} -4 \leq  \sqrt{5x+1}+2

2*\sqrt{5x+1} -\sqrt{5x+1} \leq  2+4

\sqrt{5x+1} \leq  6

возведем обе части в квадрат

5x+1 \leq  36

5x \leq  35

x \leq  7

Аноним: это как вообще
Аноним: спасибо
Похожие вопросы
Математика
1 год назад
СРОЧНО!!!!!ПОЖАЛУЙСТА​
Українська література
1 год назад
ДАЮ КРАЩУ ВІДПОВІДЬ 8. Фольклорна образність притаманна поезії: А) "Я стужився , мила , за тобою ..." Б)"Я ..." В) "Два кольори" Г)"Задивляюсь у твої зіниці ..." Д)"У синьому небі я висіяв ліс ..."​
Українська література
1 год назад
твір на тему я і волонтерство для 7 класу​
Математика
1 год назад
терміново будьласка ​
Английский язык
2 года назад
Task II. Translate from Ukrainian into English 1. Бізнес-менеджери повинні встановити чіткі фінансові цілі, щоб підкреслити фінансові цілі компанії. 2. Ми надаємо нашим працівникам високу
Русский язык
2 года назад
Выпишите из текста прилагательные и наречия в превосходной или сравнительной степени (не менее двух). Анюта бежала домой сломя голову, находясь на седьмом небе от счастья, ведь завтра в школе
Математика
8 лет назад
292903 не делится на 9 почему?
Математика
8 лет назад
Цветы 50 штук собраны в букеты по 3 штуки и по 5 штук. Сколько собрано букетов по 3 штуки, если всего 12 букетов?