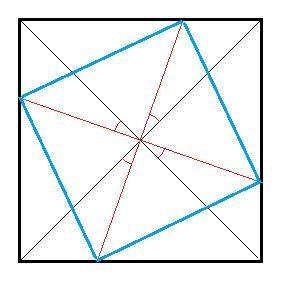
Через точку пересечения диагоналей квадрата проведены две взаимно перпендикулярные прямые. Доказать, что точки пересечения этих прямых со сторонами квадрата, являются вершинами еще одного квадрата.
Ответы
Ответ дал:
1
Диагонали делят квадрат на четыре равных треугольника.
Красные углы равны как вертикальные и как полученные вычитанием общей части из прямых углов.
Красные отрезки проведены из соответствующих вершин равных треугольников под равными углами к соответствующим сторонам, следовательно равны.
В синем четырехугольнике диагонали точкой пересечения делятся пополам - признак параллелограмма.
В параллелограмме диагонали равны - признак прямоугольника.
В прямоугольнике диагонали перпендикулярны - признак квадрата.
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад