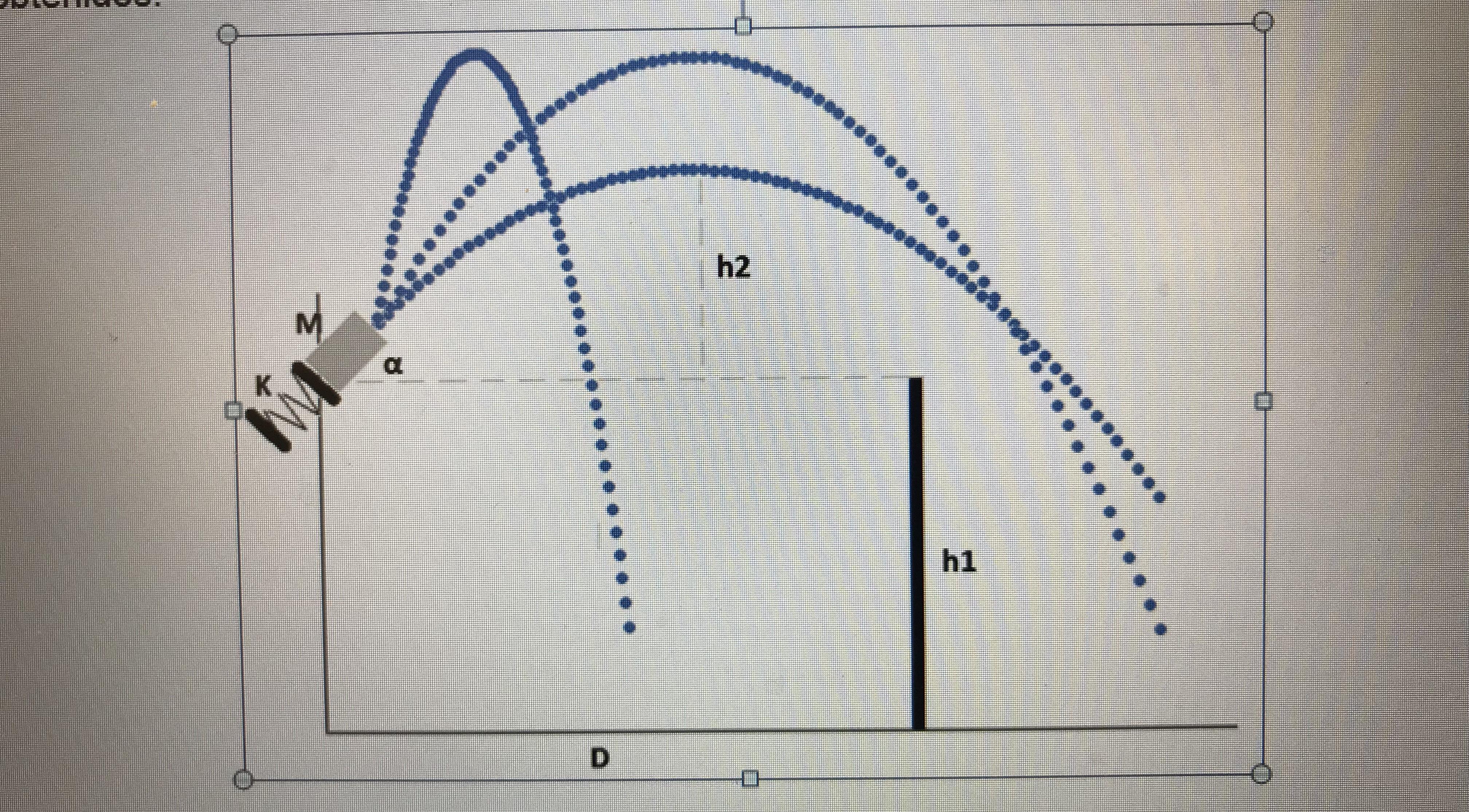
Мы хотим бросить массу M = 500 грамм над стеной высотой h1 = 5 м, расположенной на расстоянии D = 10 м, с помощью пружины упругой постоянной K = 1000 Н / м.
а) Проведите исследование траекторий на основе скорости и начального угла запуска.
б) Насколько сильно нам нужно сжать пружину, чтобы хотя бы преодолеть стену? Какую высоту h2 достигло бы в этом случае?
Приложения:
Ответы
Ответ дал:
1
Ответ:
Δx ≈ 22,4 см
Объяснение:
Высота стены в этой задаче не играет роли, т.к. пружины конец стены находятся на одном уровне. Поэтому можем воспользоваться формулой дальности броска:
L=v0²*sin(2α)/g
Как видно из формулы, максимальная дальность достигается при угле броска 45°.
Найдём из этой формулы скорость, причём эта скорость будет минимальной для того, чтобы тело перелетело стену:
v0 = √(gL) = 10м/с
Чтобы узнать, насколько нужно сжать пружины, воспользуемся законом сохранения энергии:
mv0²/2 = kΔx²/2 - формула показывает, что вся энергия пружины превратится в кинетическую энергию тела
Из этой формулы находим Δx:
Δx = v0·√(m/k) ≈ 22,4 см
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад