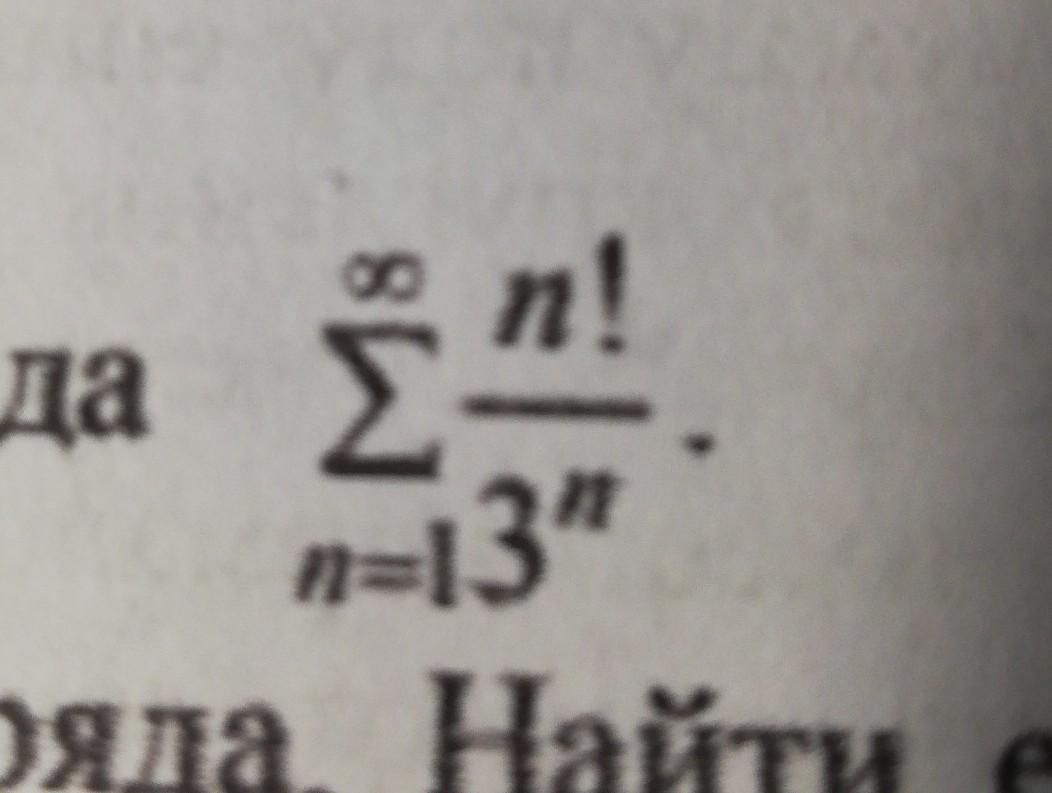• Предмет: Математика
  • Автор: artemovnikolay1
  • Вопрос задан 1 год назад
< >

срочно.
Исследовать сходимость числового ряда ​

Приложения:

Ответы

Ответ дал: Аноним
2

По признаку Даламбера:

r=\displaystyle \lim_{n \to \infty}\frac{a_{n+1}}{a_n}=\lim_{n \to \infty}\frac{(n+1)!}{3^{n+1}}\cdot \frac{3^n}{n!}=\lim_{n \to \infty}\frac{n+1}{3}=\infty &gt;1

Поскольку r > 1, то данный ряд расходится.

artemovnikolay1: еще решишь 1 пример?
Похожие вопросы
Английский язык
1 год назад
Сделать проект на тему: "почему нужно учить Английский" Условия 1.сделать в приложении (фотка снизу) 2.Отправить в виде (ссылки) 3.Постараться сделать до 01.05.23 до 16:00 ​
Физика
1 год назад
Знайти виштовхувальну силу, яка діє на тіло об'ємом 2,5 м3 занурене у воду
Английский язык
1 год назад
The pop singer _______ (dance) on the stage when she ________ (fall) over. 1)was dancing; was falling 2)was dancing; fell 3)danced; fell 4)danced; was falling
Литература
1 год назад
Чий портрет було виставлено на аукціон?,Тараса Шевченка
Русский язык
2 года назад
16. Перестройте личные предложения в безличные. Образец: Густой туман застилал долину реки. -Густым туманом застилало долину реки; На свежем воздухе люди дышали легко. - На свежем воздухе дышалось
Химия
2 года назад
Определите состав атомов следующих элементов. Ответы запишите в таблице. ​
География
8 лет назад
Подвижный участок земной коры имеющую сложную складчатую структура?
Геометрия
8 лет назад
1) Диагонали ромба 8 и 6 см. Чему равна площадь ромба? 2) Основание параллелограмма 10 см, другая сторона = 5 см. Чему равна площадь параллелограмма