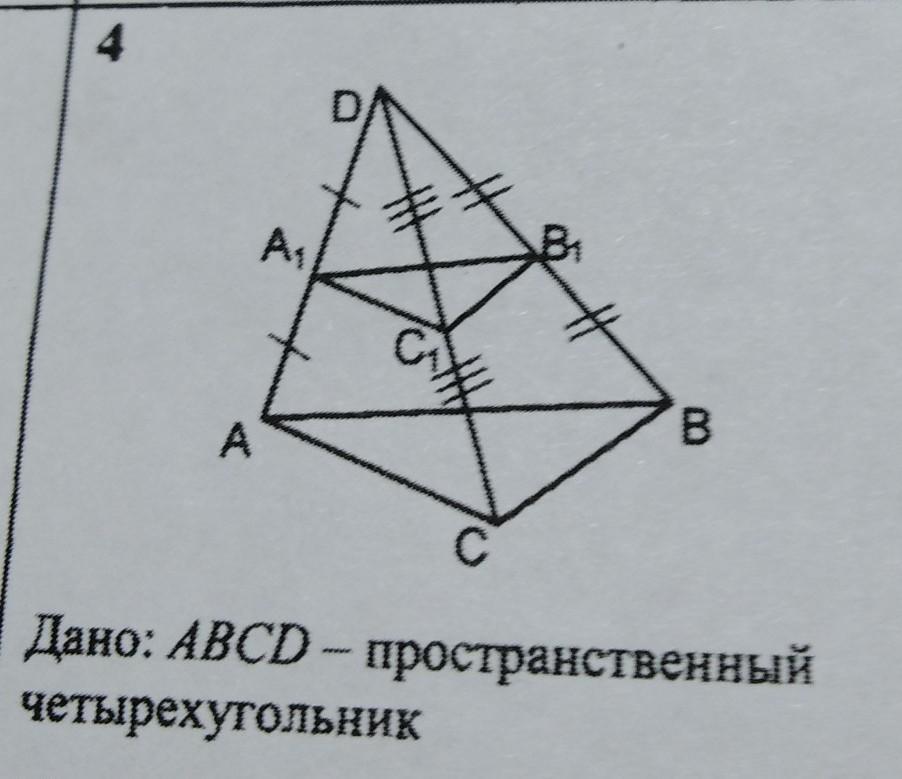
Доказать параллельность плоскостей ABC и A1B1C1
Дано: ABCD - пространственный четырёхугольник
Приложения:
Ответы
Ответ дал:
12
А1С1-средняя линия ΔADC, значит A1C1||AC
аналогично C1B1||CB; A1B1||AB
Через две пересекающиеся прямые A1C1 и А1В1 проходит единственная плоскость А1В1С1.
Есть теорема: Если две пересекающиеся прямые одной плоскости (прямые АС и АВ в плоскости АВС) параллельны двум пересекающимся прямым другой плоскости (A1C1 и А1В1 в плоскости A1B1C1), то такие плоскости параллельны.
Тогда плоскости АВС и А1В1С1 параллельны
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад