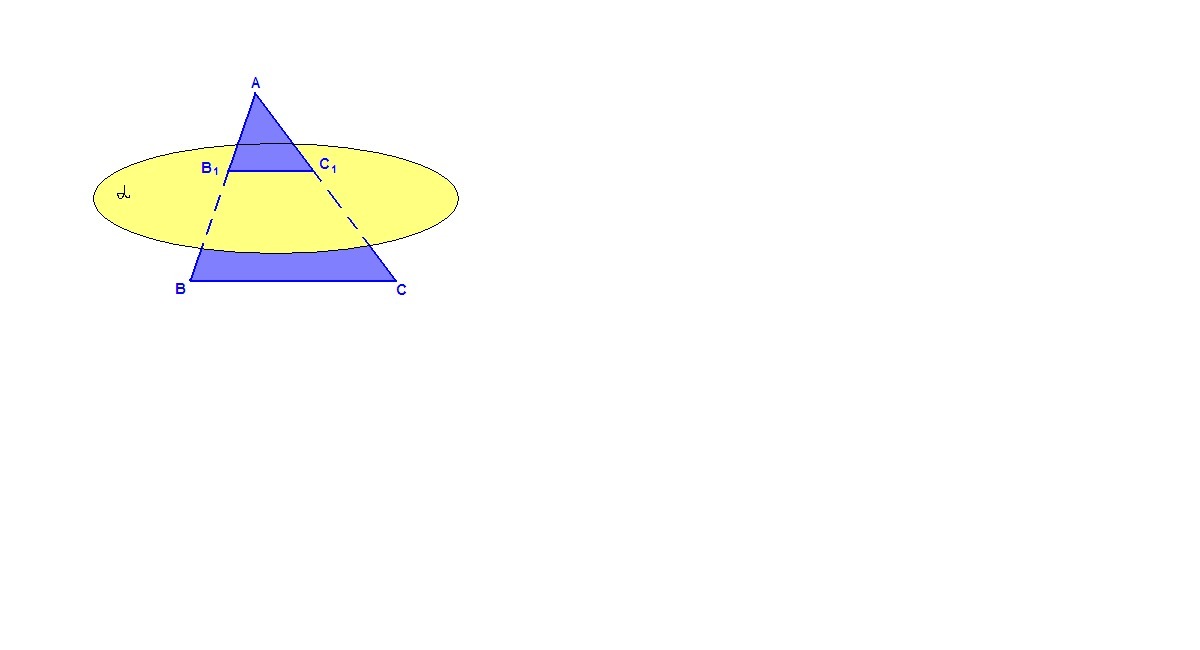
плоскость а пересекает стороны АВ и АС треугольника АВС соответственно в точках В1 С1. Известно, что ВС//а, АВ:В1В=5:3, АС=15 см. Найдите АС1

ВС║α, плоскость (АВС) проходит через ВС и пересекает α, значит линия пересечения В₁С₁║ВС.

∠АВС = ∠АВ₁С₁ как соответственные при пересечении В₁С₁║ВС секущей АВ, ∠ВАС общий для треугольников АВС и АВ₁С₁, значит эти треугольники подобны по двум углам.

АВ : ВВ₁ = 5 : 3, значит АВ₁ : АВ = 2 : 5.

Из подобия треугольников АВС и АВ₁С₁ следует, что
АС₁ : АС = АВ₁ : АВ = 2 : 5
АС₁ : 15 = 2 : 5
АС₁ = 15 · 2 / 5 = 6 см.