Знайдіть кути чотирикутника ABCD, вписаного в коло, якщо кут АDB=43°, кут ACD=37°, кут CAD=22°. (Решение пожалуйста с рисунком и дано)
Ответы
Ответ дал:
38
Ответ:
<A = 100°; <B = 59°; <C = 80°; <D = 121°
Объяснение:
Дано:
<ADB = 43°;
<ACD = 37°;
<CAD = 22°.
Знайти: <A, <B, <C, <D.
Розв’язок:
Нехай т.О - точка перетину діагоналей чотирикутника.
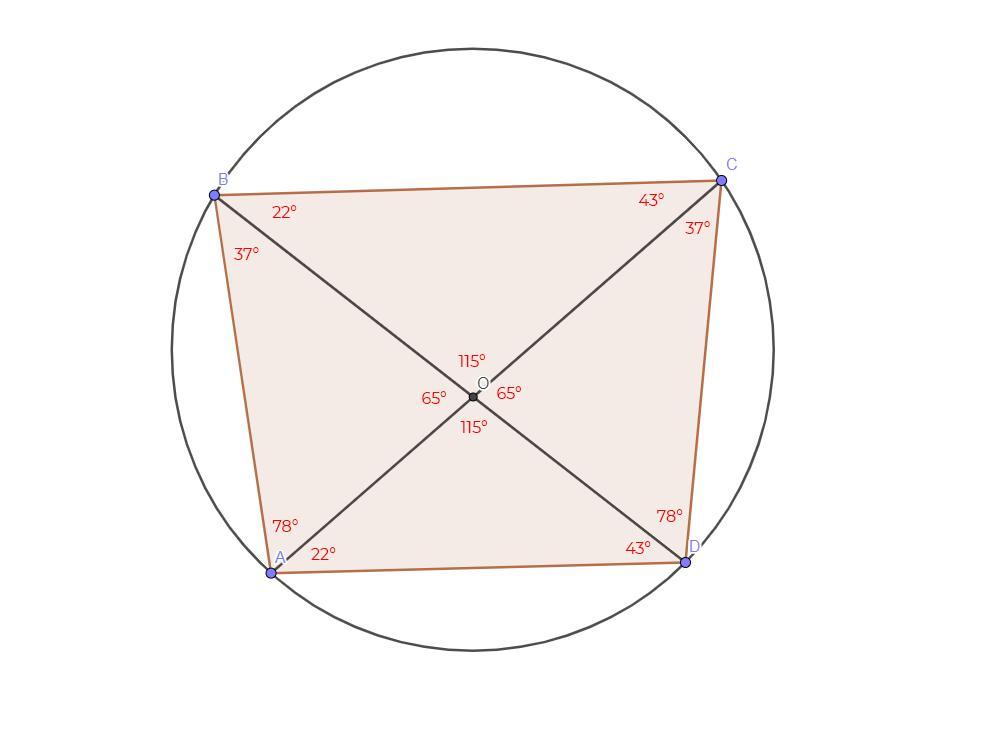
<DCA = <DBA = 37° (вписані кути, що спираються на одну дугу, рівні)
<DBC = <DAC = 22°
<AOD = 180° - 22° - 43° = 115°
<AOD + <AOB = 180° <=> <AOB = 180° - 115° = 65°
<OAB = 180° - 65° - 37° = 78°
<A = 22° + 78° = 100°
<COD = <AOB = 65°
<CDO = 180° - 65° - 37° = 78°
<D = 78° + 43° = 121°
<ACB = 180° - 115° - 22° = 43°
<C = 37° + 43° = 80°
<B = 22° + 37° = 59°
Перевірка (у вписаного чотирикутника в коло сума протилежних кутів рівна):
<A + <C = <B + <D
100° + 80° = 59° + 121°
180° = 180°
Відповідь: <A = 100°; <B = 59°; <C = 80°; <D = 121°.
Приложения:
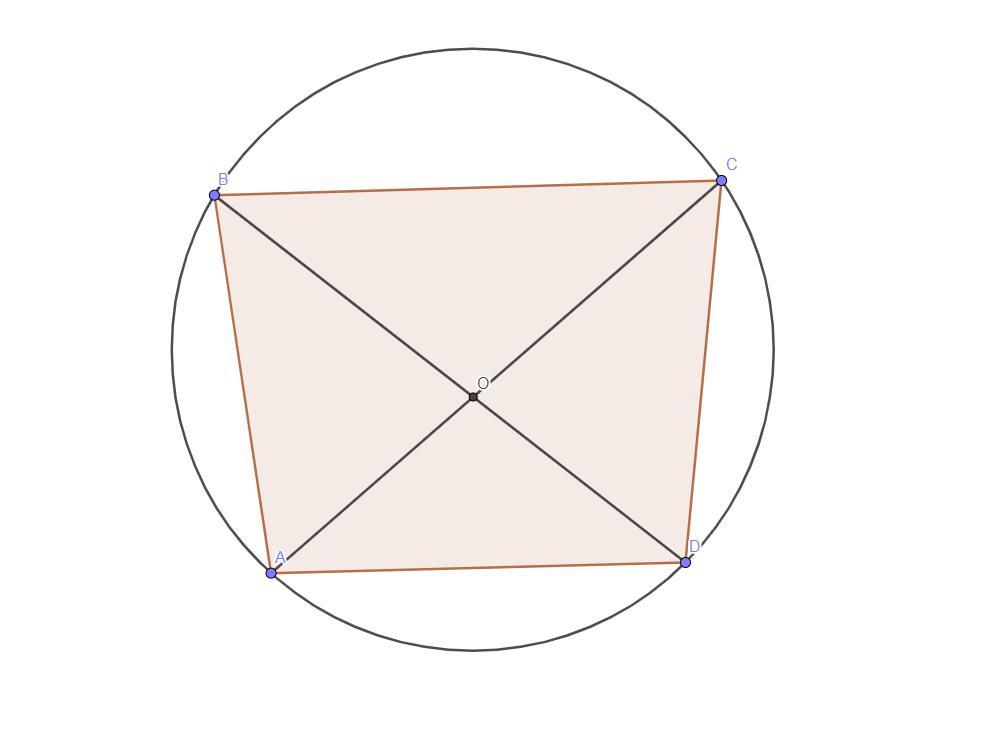
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад