в прямоугольном треугольнике угол между биссектрисой и медианой проведенными из вершины прямого угла равен 41 градус. найдите больший из двух лстрых углов треугольника
Ответы
Ответ дал:
0
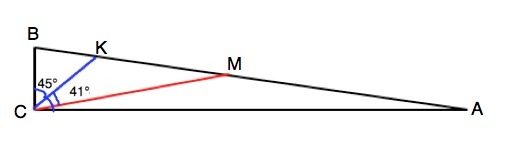
Пусть данный треугольник АВС, угол С=90°. Биссектриса СК делит его пополам.
Угол ВСК=АСК=90°:2=45°.
Медиана СМ отсекает от угла АСК 41°.
угол МСА=АСК-МСК=45°-41°=4°
Медиана прямоугольного треугольника, проведенная из прямого угла, равна половине гипотенузы. СМ=АМ
Треугольник СМА - равнобедренный. По свойству равнобедренного треугольника ∠МАС=∠МСА=4°.
Сумма острых углов прямоугольного треугольника 90°.
Угол В=90°- 4°=86°. - это больший острый угол данного треугольника.
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад