ГЕОМЕТРИЯ 7 КЛАСС ЗАДАЧА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА .Можно с подробным пояснением.

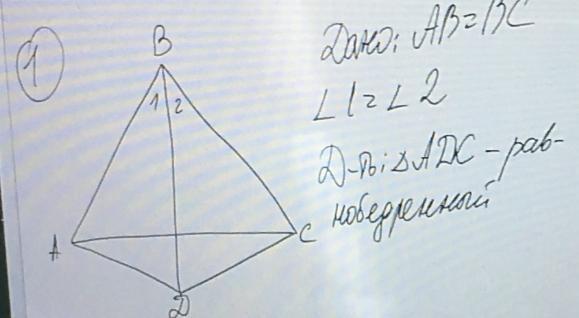
Назовём точку пересечения прямых BD и AC точкой О
Прямая BD - биссектриса угла АВС, а значит, делит четырёхугольник АВСD на равные части
Из этого следует, что прямые АD и DC равны, а значит, что треугольник равнобедренный

AB=BC => ΔABC - равнобедренный, угол ВАС равен углу ВСА.

Рассмотрим треугольники DAB и DCB.

Они равны, поскольку АВ=ВС, угол 1 равен углу 2 и BD - общая сторона.

Отсюда следует, что угол BAD равен углу BCD.

Так, теперь мы видим, что ВАD=BCD и BAC=BCA => угол CAD равен углу ACD => треугольник ADC - равнобедренный, что и требовалось доказать.