В треугольнике АВС площадь которого равна 6✓2 , АВ 9см А 45° найдите сторону АС и опущенную на неё высоту

Ответ:

см

см

Объяснение:

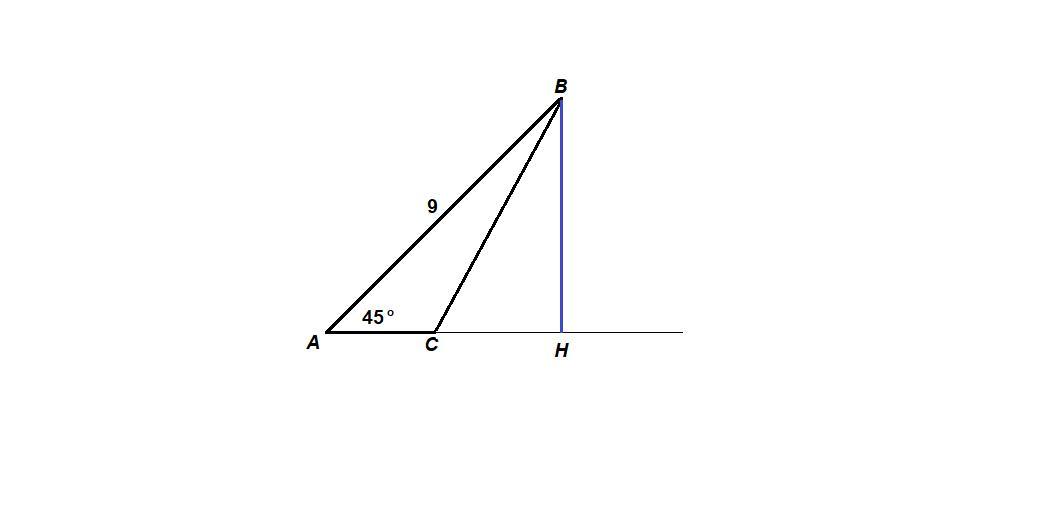
ВН - высота, опущенная на АС.

В прямоугольном треугольнике АВН ∠А = 45°, значит и ∠АВН = 45°, тогда треугольник равнобедренный,

ВН = АН = х

По теореме Пифагора AB² = AH² + BH²,

x² + x² = 81

2x² = 81

x² = 81/2

см

Площадь треугольника АВС:

см