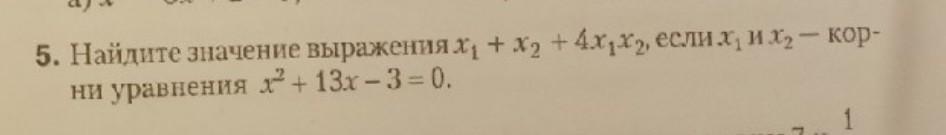Предмет: Алгебра
Автор: Аноним
Вопрос задан 1 год назад

< >

найдите значение выражения х1+х2+4х1х2, если х1 и х2- корни уравнения х^2+13х-3=0

Приложения:

Ответы

Ответ дал: sergeevaolga5

2

Ответ:

$-25$

Объяснение:

$x^2+13x-3=0\\D=13^2-4*1*(-3)=169+12=181\\\\x_{1,2}=\frac{-13\pm\sqrt{181}}{2}\\\\x_1+x_2+4x_1x_2=\\=\frac{-13+\sqrt{181}}{2}+\frac{-13-\sqrt{181}}{2}+4*(\frac{-13+\sqrt{181}}{2})(\frac{-13-\sqrt{181}}{2})=\\\\=\frac{-26}{2}+((-13)^2-(\sqrt{181})^2)=-13+169-181=-25$

Аноним: по Виета: x1+x2=-13;x1*x2=-3; x1+x2+4x1x2=-13+4*(-3)=-25

Похожие вопросы

Математика

1 год назад

У школі навчається 500 учнів, 52% з них - дівчата. Скільки хлопців у школі

Физика

1 год назад

чи вийде світловий промінь із діаманту у повітря, якщо кут падіння 40 градусів

Українська література

1 год назад

терміново план до твору пам'ятник Богдану Хмельницькому. Будь-ласка допоможіть

География

1 год назад

За картою визначте відстань у градусах від початкового меридіана до меридіана, на якому розташоване місто Київ

Алгебра

2 года назад

-6m^3n^2-9m^2n-18mn^2 (a^2-2a)^2 Нужно вынести общий множитель за скобки . срочно плиз

История

2 года назад

1. Расположите события в хронологической последовательности. А) Взятие Иерусалима крестоносцами Б) Разгром крестьянского-ополчения крестоносцев турками-сельджуками В) Создание Иерусалимского

География

8 лет назад

определите уклон волги если высота истока 250м а высота усттья 28м

Алгебра

8 лет назад

y=(3-x)(x+2)(x+1)/x+2 постройте график