Решить неопределенный интеграл.

theclosenone: я в самом начале сделал замену t = (x+3), dx=dt потом
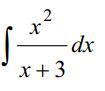
х = (t-3). получилось ∫(x^2/x+3)dx = ∫(x^2/t)dt = ∫((t-3)^2/t)dt = ∫(t^2-6t+9/t)dt = ∫(t^2/t - 6t/t + 9/t)dt = ∫(t-6+9t^-1)dt= t^2/2 - 6t + 9 ln | t | + C = (x+3)^2/2 - 6(x+3) + 9 ln | x + 3 | + C.
теперь думаю кто из нас верно решил...некоторые моменты как и в моем способе решения так и в вашем сходится. объясните пожалуйста как вы решали данный интеграл?

igorShap: А Вы раскройте скобки и соберите все константы в одну. Получите тот же ответ(с точностью до константы, конечно)

igorShap: К слову, смотрел у Вас только результат, промежуточные действия не могу пока проверить