Три покупателя независимо друг от друга могут сделать по одной покупке в магазине. Вероятность того, что покупку сделает первый покупатель, равна 0,6, второй – 0,8, третий – 0,9. X – число покупок, сделанных этими покупателями. Найти ряд и функцию распределения для Х, а также МХ, DX и вероятность того, что Х не меньше 2

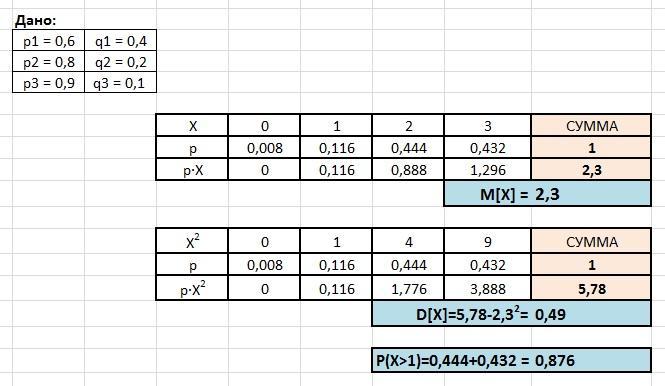
Решим задачу в Excel (см. приложение)

Необходимые пояснения:

Вероятность покупки (и не покупки):

p₁ = 0,6;     q₁ = 1 - p₁ = 0,4

p₂ = 0,8;     q₂ = 1 - p₂ = 0,2

p₃ = 0,9;     q₂ = 1 - p₃ = 0,1.

Ряд распределения.

Число покупок:

X₀ = 0 - покупок не сделано;

X₁ = 1 - покупка  сделана только одним покупателем;

X₂ = 2 - покупку  сделали двое покупателей;

X₃ = 3 - покупку  сделали все покупатели.

Функция распределения.

Всевозможные исходы:

P₀ = q₁·q₂·q₃ = 0,008;

P₁  = p₁·q₂·q₃ +  q₁·p₂·q₃ +  q₁·q₂·p₃ = 0,116;

P₂  = p₁·p₂·q₃ +  p₁·q₂·p₃ +  q₁·q₂·p₃ = 0,444;

P₃ = p₁·p₂·p₃ = 0,432.

Проверка:

0,008+0,116+0,444+0,432 = 1

Математическое ожидание:

M[X] = 0·0,008 + 1·0,116 + 2·0,444 + 3·0,432 = 2,3

Дисперсия:

D[X] = 0²·0,008 + 1²·0,116 + 2²·0,444 + 3²·0,432 -  2,3² = 0,49

Вероятность

P(x>1) = 0,444+0,432=0,876