• Предмет: Алгебра
  • Автор: slavachimbuev
  • Вопрос задан 1 год назад
< >

Найти производную функции
У=arctg x/√8-x^2

slavachimbuev: Можете пожалуйста сказать откуда ответы? Очень нужно на экзамен

Ответы

Ответ дал: NNNLLL54
1

y=\frac{arctgx}{\sqrt{8-x^2}}\\\\y'=\frac{\frac{1}{1+x^2}\cdot \sqrt{8-x^2}-arctgx\cdot \frac{1}{2\sqrt{8-x^2}}\cdot (-2x)}{8-x^2}=\frac{8\, -\, x^2\, +\, x\cdot (1+x^2)\, \cdot \, arctgx}{(1+x^2)\, \sqrt{(8-x^2)^3}}

Ответ дал: Аноним
0

Два варианта ответов. Первый при условии, что дан арктангенс, а второй - дробь, в котором арктангенс в числителе...

Приложения:
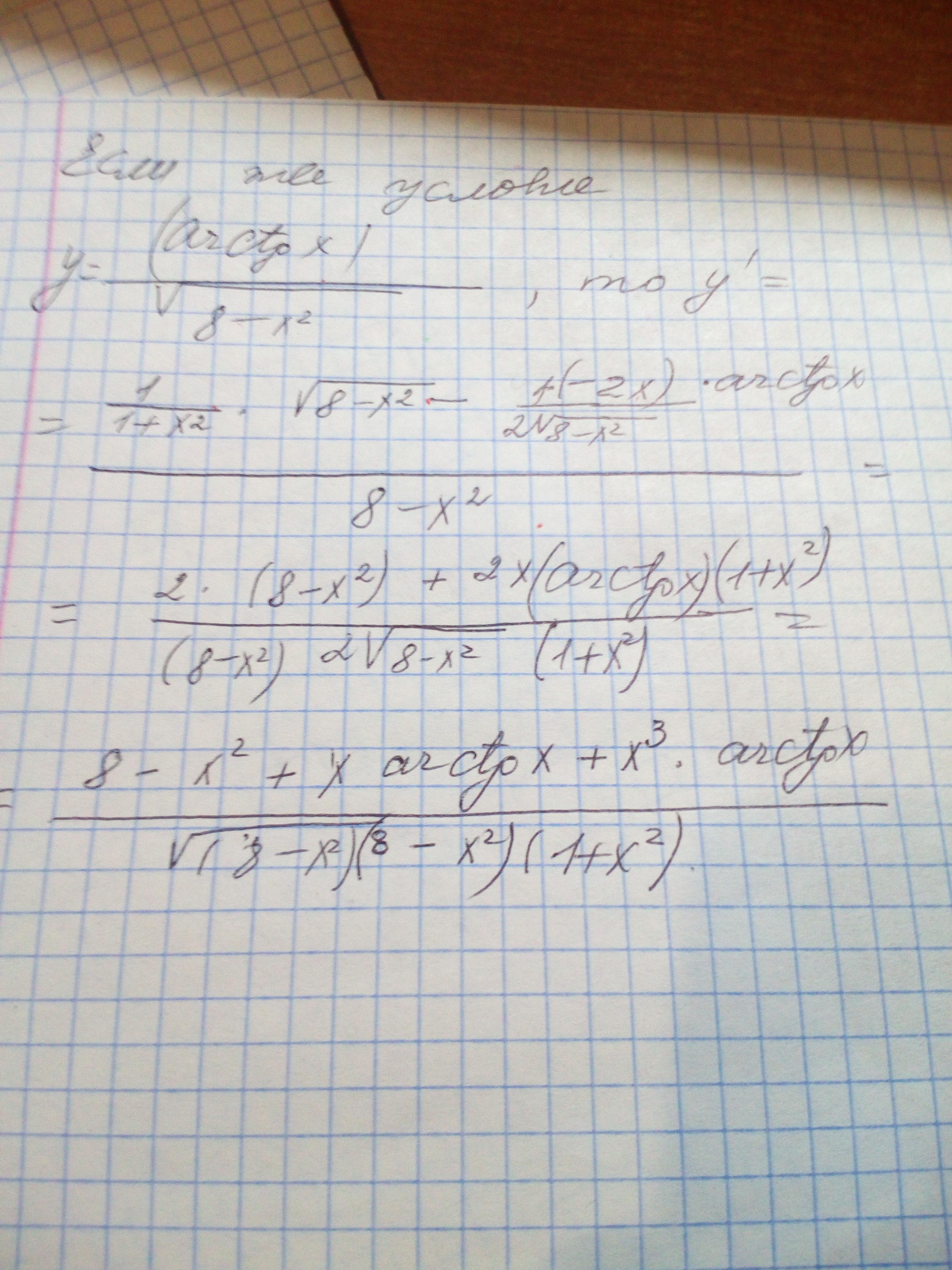
Похожие вопросы
Русский язык
1 год назад
Помогите пожалуйста.
Математика
1 год назад
рого рав 952. Выполните действия: 3,3 +126 13 30 1) 4- 9 02 . 1,5 60; 2) 2,07. 3 7 + 2,9: 0,52 19; 4) 17- 22 : 9 29 66 75.6 36,75-60. 2.​
Українська література
1 год назад
(Бали: 12) Запиши на надішли на перевірку відео вивченого напам’ять вірща. Відео необхідно завантажити в цьому ДЗ. Тарас Шевченко «Як умру, то поховайте…» Зауваження. При завантаженні
Українська мова
1 год назад
8. Тире між підметом та присудком потрібно у реченнях, окрім А Народна пісня духовне обличчя нації. Б Люди господарі своєї долі (В. Шекспір). В Цей край мій. Г Співати рідний край прославляти.​
Химия
2 года назад
Отметь неверно составленную формулу: 1)N2O 2)P2O5 3)FeO 4)KO Запиши эту формулу правильно.
Окружающий мир
2 года назад
Ребят помогите пж всё это сделать Даю 40 баллов!!!!!!!!! Не шучу!!! Пж
Физика
8 лет назад
Определить силу реакции опоры если сила трения скольжения 50 Н а коэф трения 0.5
Литература
8 лет назад
Помогите написать сочинение на тему " Что увидел и узнал Мцыри за три дня свободной жизни" План 1)Поэма Лермонтова "Мцыри"- поэма о свободной личности 2) Три дня странствий а)история Мцыри.Причины