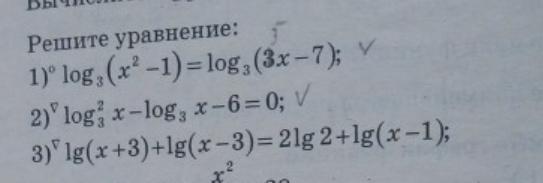Ответы
Ответ:
1.
Нет корней.
2.
х1 = 1/9
х2 = 27
3.
х = 5
Объяснение:
1.
Для начало О.Д.З.
х² - 1 > 0, x² > 1, x > 1 или х < -1.
3x - 7 > 0, 3x > 7, x > 7/3.
x ∈ (7/3; ∞).
1-й способ.
Пусть log[3](х² - 1) = а, 3^а = х² - 1.
Пусть log[3](3х - 7) = в, 3^в = 3х - 7.
Тогда а = в и 3^a = 3^в.
Следовательно, х² - 1 = 3х - 7
х² - 3х + 6 = 0
D отрицательный, корней нет.
2-ой способ.
Для начало О.Д.З.
х > 0.
x > 0.
x ∈ (0; ∞)
По свойству log, при сложении, вычитании log с равной степенью их аргументы умножаются, делятся.
log[x](а) + log[х](5р + 3) = log[x](а * (5р + 3)) = log[х](5ар + 3а).
log[x](а) - log[х](5р + 3) = log[x](а / (5р + 3)).
В даном примере придётся делить.
log[3](х² - 1) - log[3](3х - 7) = 0
log[3]((х² - 1) / (3х - 7)) = 0
3^0 = (х² - 1) / (3х - 7)
(х² - 1) / (3х - 7) = 1
х² - 1 = 3х - 7
х² - 3х + 6 = 0
D отрицательный, корней нет.
2.
Решается как самое простое квадратное уравнение, нужно просто провести замену и решить через какуету новою переменную, обычно используют переменную t.
Пусть log[3](x) = t
Тогда t² - t - 6 = 0
Решив это уравнение, вы получите t1 = -2, t2 = 3.
Получается log[3](x) = -2 или log[3](x) log[3](x) = 3.
3^(-2) = 1/9 или 3³ = 27
х1 = 1/9
х2 = 27
3.
Для начало О.Д.З.
х + 3 > 0, x > -3.
x - 3 > 0, x > 3.
x - 1 > 0, x > 1.
x ∈ (3; ∞).
㏑(((х + 3) * (х - 3)) / (х - 1)) = 2㏑(2)
㏑((х² - 9) / (х - 1)) = ㏑(2) + ㏑(2)
㏑((х² - 9) / (х - 1)) = ㏑(4)
Это уравнение похоже на 1-ое и решается также двумя способами, но в итоге всё придёт к тому, что ((х² - 9) / (х - 1)) = 4.
х² - 9 = 4 * (х - 1)
х² - 9 = 4х - 4
х² - 4х - 5 = 0
Решив это уравнение, вы получите х1 = -1, х2 = 5.
х1 = -1 не входит в О.Д.З.
Следовательно, х = 5.