Ответы
Ответ дал:
1
Ответ:
Объяснение:
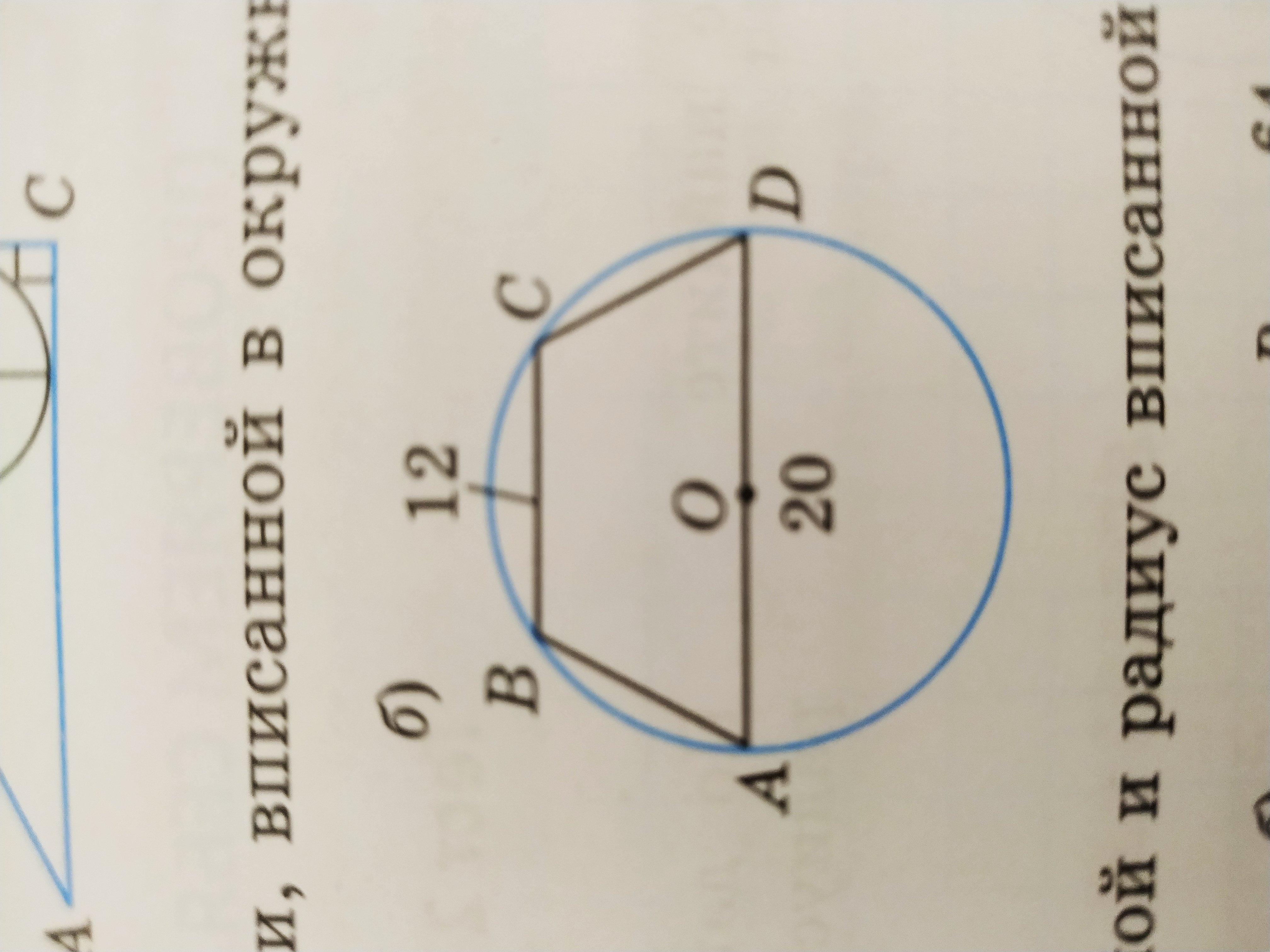
Пусть СК⊥АД, ВР⊥АД. Тогда КР=12, РД=АР=(20-12)/2=4.
В ΔАСД , ∠АСД=90, т.к он вписанный и опирается на полуокружность с градусной мерой 180.
ΔАСД-прямоугольный . Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу : СК=√(АК*КД)=√16*4=4*2=8
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад