Помогите решить уравнение
Приложения:
Аноним:
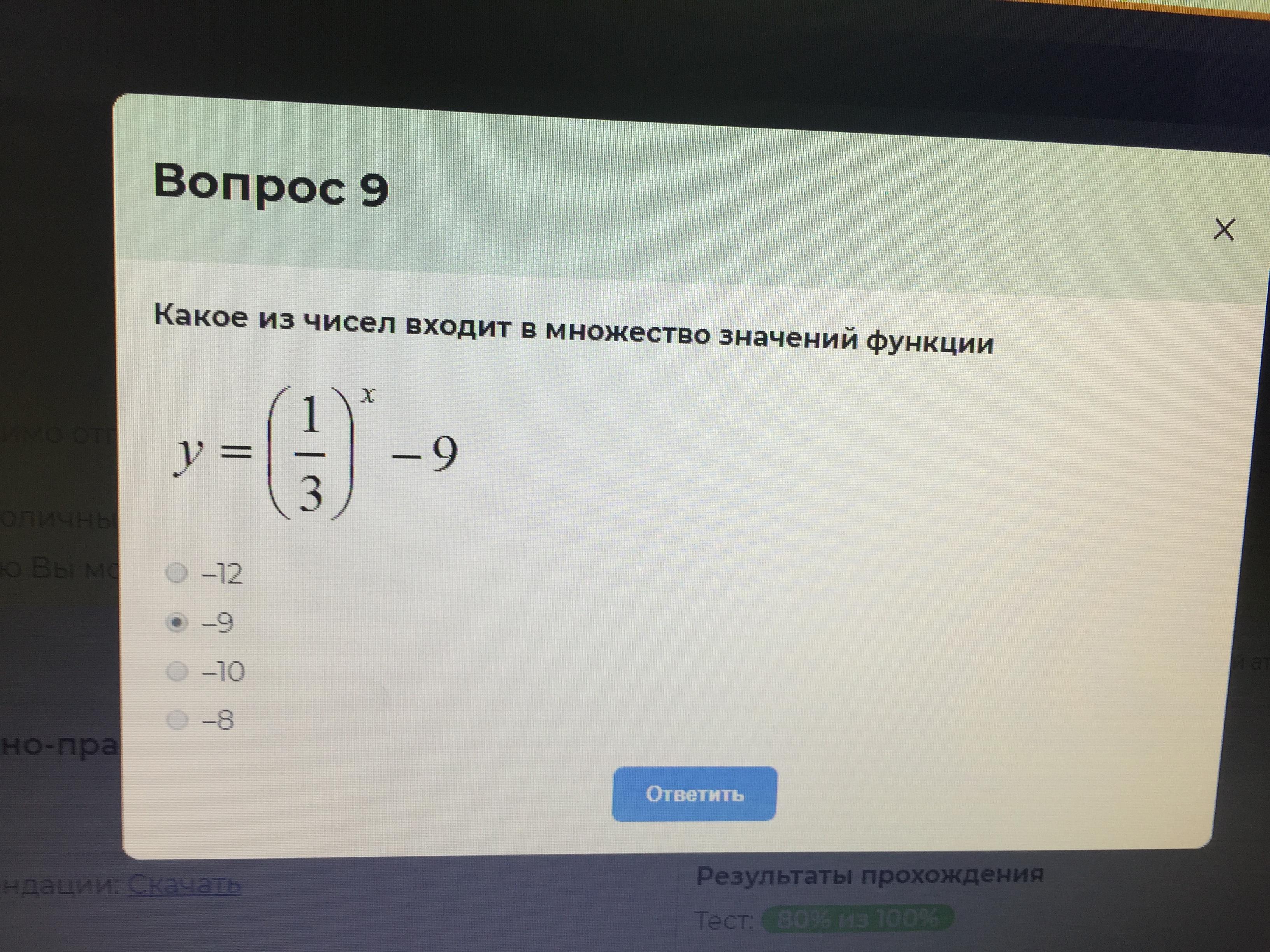
Это не уравнение, а покащательная функция. Нужно знать график и тогда легко записать область значений. Область значений функций у =(1/3)^х: Е(у) =(0; +бесконеч). Тогда область значений данной функции (-9; +бесконечность). В этот промежуток входит число -8.
"показательная"
Ответы
Ответ дал:
1
y = (1/3)^x-9. Множество значений функции ,можно представить ,как все значения y при которых можно найти x,т.е x должен входить в область определения ,заменим y на a:
a = (1/3)^x - 9 , a+9 = 1/(3^x), 3^x = 1/(a+9) , ln(3^x) = ln(1/(a+9))
x*ln(3) = ln (1/(9+a) ==> x = ln(1/(9+a))/ln(3)
Отсюда следуют ограничения : 9+a≠0 и 1/(9+a) >0 .Решая эту систему неравенств получаем , что a ≠-9 и a>-9. или y > -9
Ответ : в множество значений функции входит -8
Это решение как с Тулы в Москву через Камчатку. А если ещё и не учили логарифмы, то как через Америку.
Разве в тесте важно решение?
Это выбор автора вопроса, пусть что хочет, то и переписывает.
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад