Какая наибольшая площадь может быть у треугольника, если длины двух его медиан равны 14 и 18, а угол между ними равен 150

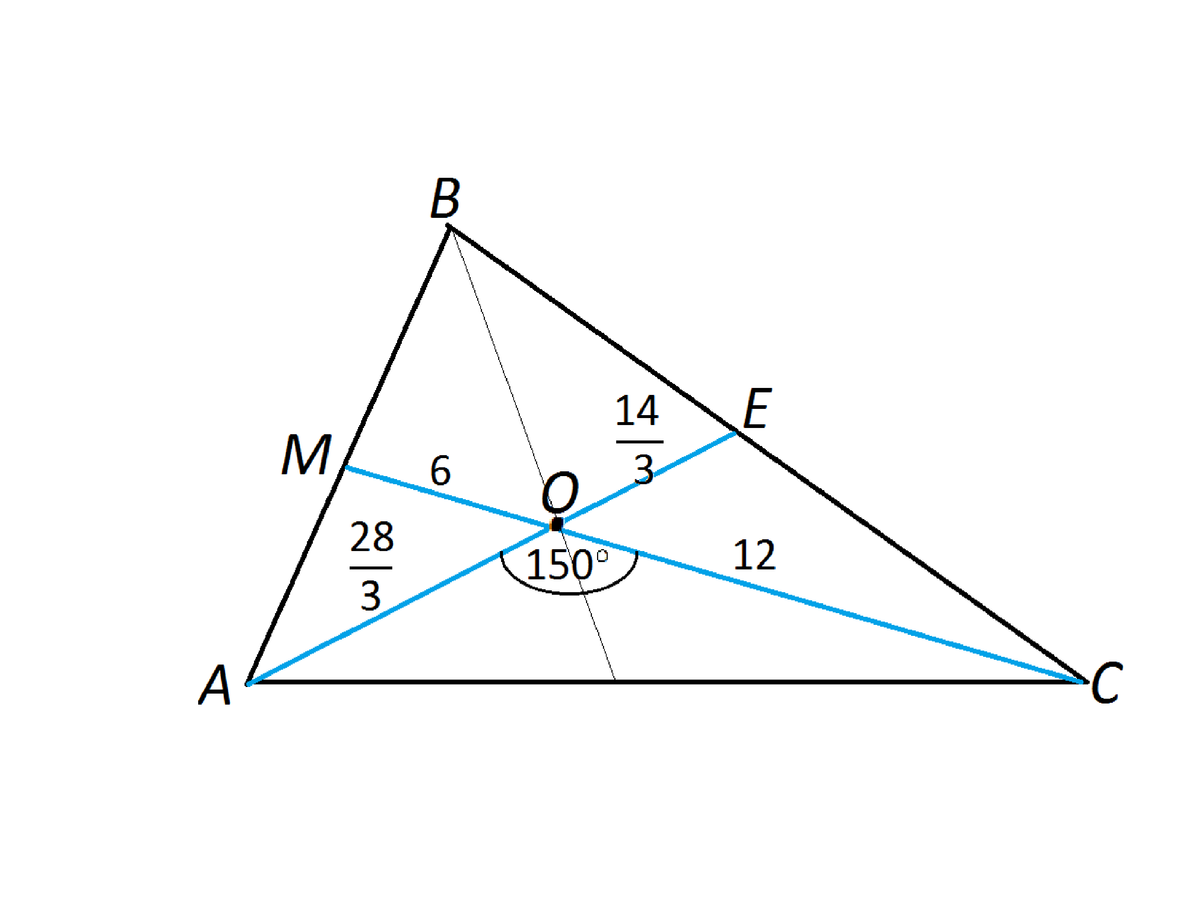
Пусть данный треугольник будет АВС, точка пересечения медиан О.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. 
АО=14:3*2=28/3 
СО=18:3*2=12
Медианы делят треугольник на равновеликие треугольники.
Три медианы делят его на 6 равновеликих треугольников. 
Если мы проведем из В к АС еще одну медиану, то
S Δ АОС будет равен 2/6 площади Δ АВС, т.е. 1/3
Площадь треугольника равна половине произведения двух его сторона на синус угла, заключенного между ними. 
Найдем площадь Δ АОС:
S ΔAOC=AO*OC*sin(150°):2=28*12:(3*2*2)=28
S ΔABC=3* S ΔAOC=28*3=84 единиц площади.