Предмет: Математика
Автор: fdkjdkfj
Вопрос задан 1 год назад

< >

Математика (помогите решить , не спамить)
Вычислить по формуле Муавра - z^5
комплексное число z=5корень3+5i

Приложения:

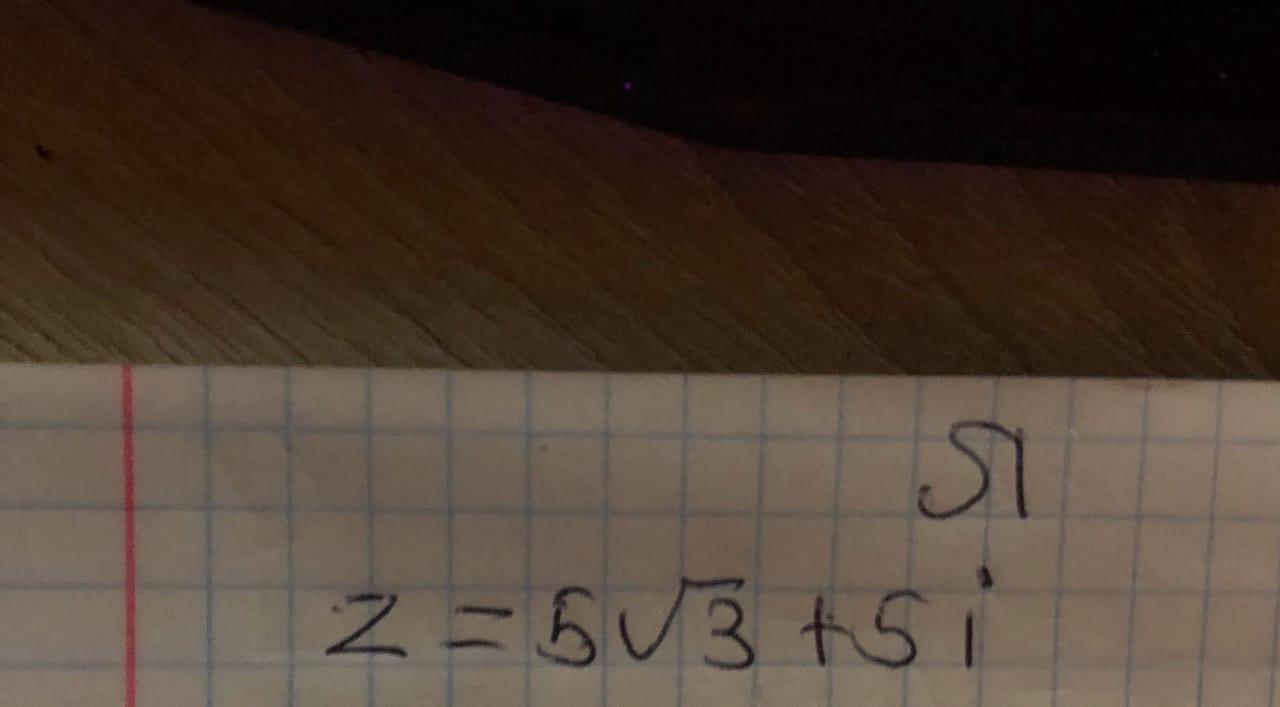
Ответы

Ответ дал: sergeevaolga5

1

Ответ:

$-50000\sqrt{3}+50000i$

Пошаговое объяснение:

$z=5\sqrt{3}+5i\\\\a=5\sqrt{3},\;b=5\\|z|=\sqrt{a^2+b^2}=\sqrt{(5\sqrt{3})^2+5^2} =\sqrt{25*3+25}=\sqrt{100}=10\\\\cosa=a/|z|=5\sqrt{3}/10=\sqrt{3}/2\;|\\sina=b/|z|=5/10=1/2\;\;\;\;\;\;\;\;\;|=>a=\frac{\pi}{6}\\\\z=|z|(cosa+isina)\\\\z=10(cos\frac{\pi}{6}+isin\frac{\pi}{6})\\\\z^5=|z|^5(cos(5a)+isin(5a)\\z^5=10^5(cos\frac{5\pi}{6}+isin5\frac{\pi}{6})=10^5(-\frac{\sqrt{3}}{2}+\frac{1}{2}i)=-50000\sqrt{3}+50000i$

Похожие вопросы

Английский язык

1 год назад

ПОМОГИТЕ СРОЧНО!!!((( Раскройте скобки в условных предложениях I, II, III типа и поставьте глаголы в правильную форму. 1.If he … (practice) every day, he … (become) a champion. (Если он будет

Математика

1 год назад

8,5x-4,9x=12,24 ПОМОГИТЕ

Химия

1 год назад

Серед наведених формул речовин КСІ, КОН, НСl - рН< 7 має розчин.

Немецкий язык

1 год назад

срочно!! пожалуйста, даю сорок баллов

Литература

2 года назад

любимый эпизод из Швайки ЛЮБОЙ!!!

Химия

2 года назад

ПОМОГИТЕ ПОЖАЛУЙСТА!!! Если в контакте находятся: А) железо и медь; Б) цинк и олово; В) железо и свинец Какой из двух металлов будет разрушаться? И почему?

История

8 лет назад

напишите причины столетней войны, напишите кратко ход войныи к моменту появлению жанны дарк очень кратко

Алгебра

8 лет назад

Срочно!!! Помогите))