Сторона квадрата ABCD равна 6 см, из т.О пересечение диагоналей квадрата, к его плоскости проведем перпендикуляр СО. Найти длину отрезка СО,если угол САО равен 60 градусов. С рисунком.

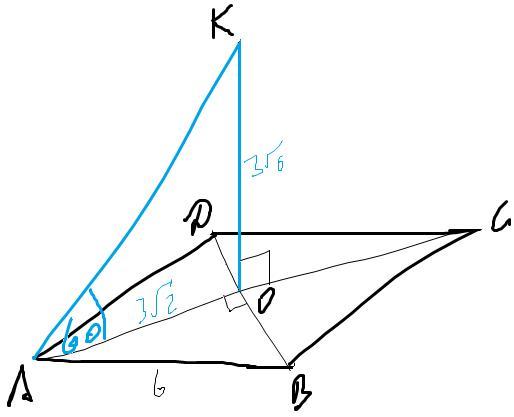
Пусть KO - искомый перпендикуляр, KAO=60.  

Диагонали квадрата перпендикулярны, равны, точкой пересечения делятся пополам.

AO =AB V2/2 =6*V2/2 =3V2 (половина диагонали квадрата)

Прямая KO перпендикулярна плоскости (ABC) и любой прямой в этой плоскости.

AOK=90

Треугольник KAO c углами 60, 90 - стороны относятся как 1:V3:2

KO =AO V3 =3V2*V3 =3V6 (см)