Помогите пожалуйста решить.Найти работу, производимую силой (Fx, Fy) вдоль дуги параболы y=x2 от точки с абсциссой x=0 до точки с абсциссой x=1.
Fx=6x–3y+10, Fy=10x+4y–1..
Я так поняла что нужно найти интеграл по формуле $\int\limits^1_0 {} (6x-3y+10)\, dx+(10x+4y-1)dy=?$

Приложения:

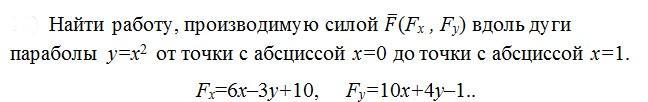
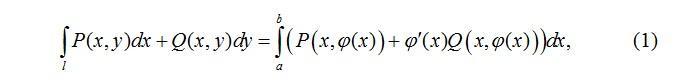
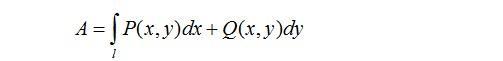
Ответы

Ответ дал: Аноним

Ответ:

$\frac{59}{3}$

Пошаговое объяснение:

Дифференциал работы - это скалярное произведение вектора силы на дифференциал перемещения:

$dA=F\cdot dr=F_x dx+F_y dy$

При этом мы знаем, что $y=x^2$ , то есть $dy = 2 x dx$

Итоговое выражение для работы:

$A=\int_0^1(6x-3x^2+10)+2x(10x+4x^2-1) dx=\frac{59}{3}$

ЮкиКросс: А можете пожалуйста расписать пошагово как именно вы нашли интеграл 59/3?

Аноним: Раскрываете скобки. После этого остается взять интеграл от многочлена. Есть общая формула для интеграла от x^n: x^(n+1) / (n+1). По ней интегрируете весь многочлен.

ЮкиКросс: окей,спасибо.

Похожие вопросы

Математика

1 год назад

Помогите 56:99 = ???

Математика

1 год назад

18sin^2x-3cosx-8=0 Помогите пожалуйста решить

Окружающий мир

1 год назад

6) Обери та підкресли правильну відповідь. Яку посудину ти обереш для приготування гарячої стра- металеву з дерев'яною ручкою чи дерев'яну з металевою ви - ручкою? - Поясни свій вибір.

Математика