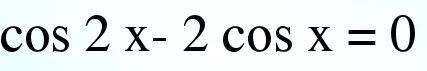Предмет: Математика
Автор: dsalo1418
Вопрос задан 1 год назад

< >

$cos2x-2cosx=0$

Приложения:

luphemalc: что нужно сделать?

dsalo1418: Найти х

Ответы

Ответ дал: Artem112

0

$\cos2x-2\cos x=0$

Распишем косинус двойного угла:

$2\cos^2x-1-2\cos x=0$

$2\cos^2x-2\cos x-1=0$

Решим квадратное уравнение:

$D_1=(-1)^2-2\cdot(-1)=3$

$\cos x_1\neq \frac{1+\sqrt{3}}{2} >1$

$\cos x_2= \frac{1-\sqrt{3}}{2}$

$x=\pm\arccos\frac{1-\sqrt{3}}{2} +2\pi n, \ n\in \mathbb{Z}$

Ответ: $\pm\arccos\frac{1-\sqrt{3}}{2} +2\pi n, \ n\in \mathbb{Z}$

Похожие вопросы

Информатика

1 год назад

помогите пж............................ даю 50б

Математика

1 год назад

У саду росло 140 дерев, з них 30% становили вишні. Обчисліть, скільки вишень росло у саду. А 48 Б 42 В 50 Г 46

Математика

1 год назад

в коробке шоколадных конфет 9 конфет из белого шоколада, что составляет 30% всех конфет в коробке. Найдите сколько всего конфет в коробке.

Математика

1 год назад

3x-15 x+7 = 0 Розв'яжіть рівняння.

География

2 года назад

На файле нижче прикрепленний 6 вопрос только.

Математика

2 года назад

Составьте задачу, решением которой будут следующие выражения: a)140:7/9 b)300:3/10

Биология

8 лет назад

По употребляемой пищи в какому типу животных относится бурый медведь?

Математика

8 лет назад

помогите решить комбайн першого дня намолотив 12т 35ц зерна пшениці,другого -на 47ц більше ,а третього -на 10т 565 кг менше,ніж пршого і другого дня разом.Яку масу зерна зібрали за три дні?