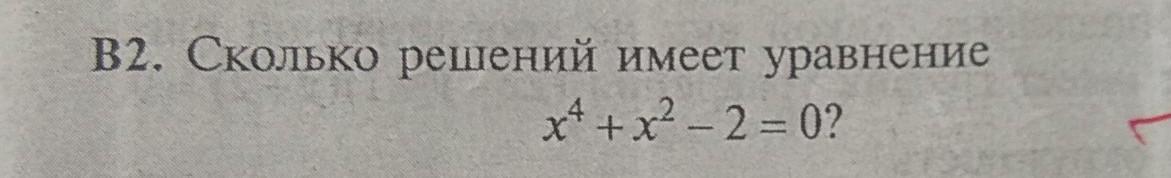• Предмет: Алгебра
  • Автор: ancordrarp9apbs
  • Вопрос задан 1 год назад
< >

сколько решений имеет уравнение ​

Приложения:

Ответы

Ответ дал: qqwairz
1

x^4+x^2-2=0

Это биквадратное уравнение, нужно произвести замену x^2 на t. Итак, t=x^2

t^2+t-2=0

t=-2

t=1

x^2=-2

x^2=1

x=-1

x=1

Ответ: уравнение имеет 2 корня, (-1;1).

bertain: Нет, число в квадрате НЕ может быть равно отрицательному числу, следовательно, x^2=-2 НЕ имеет корней. И тогда ответ: 1 решение
bertain: Таки два решения (-1 и 1), прошу прощения. Почему-то подумала, что х=-1 относится к тому уравнению, что выше
Ответ дал: bertain
1

x^4+x^2-2=0

Сделаем замену: x^2=t. Тогда:

t^2+t-2=0

D=1^2-4*1*(-2)=1+8=9

\sqrt{D} = 3

t_1=\frac{-1-3}{2} =\frac{-4}{2}=-2

t_2=\frac{-1+3}{2}=1

Возвращаемся к замене t=x^2:

x^{2} \neq -2 (число в квадрате всегда положительное)

x^2=1

x_1=-1; x_2=1

Ответ: уравнение имеет два корня.

Похожие вопросы
История
1 год назад
як розвивалась культура у 18 столітті​
История
1 год назад
Установіть хронологічну послідовність подій: А відкриття Харківського університету; Б видання Емського указу; В реформи П.Столипіна; Г видання "Русалки Дністрової".
Химия
1 год назад
Синквейн на тему "Парниковый эффект"
Английский язык
1 год назад
Помогите мне пожалуйста. Выбрать модальный глагол
Математика
2 года назад
пожалуйста правильно полностью действия и как объясните​
Английский язык
2 года назад
Срочно нужна помощь!!!​
Математика
8 лет назад
Величина угла AOC равна 140° (градусов). Найдите величину угла BOC. СРОЧНОООО
Литература
8 лет назад
СРОЧНО! Помогите пожалуйста!Дам 35 баллов! Напишите сочинение на тему "История России как одна из традиционных тем русского фольклора в произведениях Пушкина и Лермонтова" Большое спасибо!